3. НЕКОТОРЫЕ СВОЙСТВА СИСТЕМЫ МАГИЧЕСКИХ КВАДРАТОВ.

1. Программа для компьютера.
   1. Классы квадратов (повороты и симметрии).
   2. Группы квадратов (местоположение числа F).
   3. Базовые элементы квадрата и вычисление производных.
   4. Магические подквадраты.
   5. Последовательность вычислений производных элементов.
2. Результаты, выданные компьютером.
3. Преобразования множеств классов K₄₁ и K₄₃ друг в друга.
4. Преобразования множеств классов S₄₁S₄₂ и S₄₂S₄₃.
5. Кое-что о булевых алгебрах.
6. Система преобразований .
7. Интерпретации булевой алгебры.
   1. Алгебра множеств.
      1. Картинка логических операций.
      2. Взаимно-однозначность преобразований .
      3. Число разных значений преобразований .
      4. Алгебра подматриц матрицы 2x2.
   2. Алгебра элементов тетраэдра.
      1. Элементы тетраэдра как логические функции.
      2. Логические операции над элементами тетраэдра.
      3. Число преобразований разных типов.
8. Центрально-симметричные квадраты.
   1. Магические четвёрки чисел.
   2. Число центрально-симметричных квадратов.
9. Преобразования и размещения с повторениями.
10. Перестановочные преобразования.
    1. Группа перестановочных преобразований.
    2. Сохранение центральной симметрии.
    3. Система образующих.
    4. Преобразование клеток и преобразование чисел.
    5. Магичность преобразований .
    6. Структура группы перестановочных преобразований.
11. Система преобразований .
12. Условие взаимно-однозначности преобразований .
13. Инвертирующие преобразования.
    1. Группа инвертирующих преобразований.
    2. Сохранение центральной симметрии.
    3. Система образующих.
    4. Магичность преобразований T.
    5. Структура группы инвертирующих преобразований.

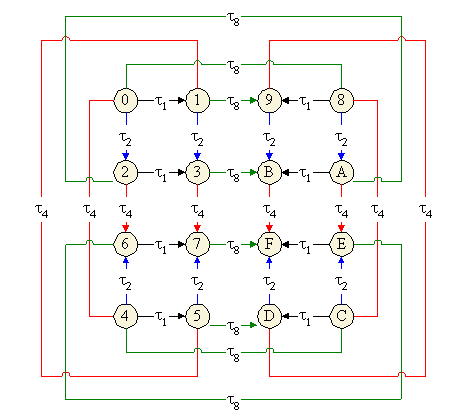
До этого места я рассматривал различные частные нумерологические свойства магического квадрата логических операций. Вообще "нумерологичность", видимо, тесно связана с симметрией. Связана ли с нею "логичность"? Попытаюсь сделать некоторые обобщения. Меня будет интересовать не столько общая теория магических квадратов 4-го порядка, сколько те магические квадраты, которые демонстрируют с помощью симметрий различные естественные свойства системы логических операций, а также те преобразования квадратов, которые имеют естественный смысл как преобразования логических операций. В то же время интересно, какое место такие "логические" квадраты и такие "логические" преобразования занимают в общих системах магических квадратов и их преобразований.

3.1. Программа для компьютера.

Мне пришлось написать специальную программу для компьютера, чтобы найти все магические квадраты 4-го порядка. Алгоритм основан на следующих идеях.

3.1.1. Классы квадратов (повороты и симметрии).

С помощью поворотов на 90^o и симметрии относительно вертикальной (или горизонтальной) оси из каждого магического квадрата можно получить ещё 7 магических квадратов. Всё множество магических квадратов 4-го порядка M₄ этими преобразованиями разбивается на множество K₄ классов по 8 квадратов в каждом. Вот схемы двух базовых преобразований:

90 поворот по часовой стрелке на 90o

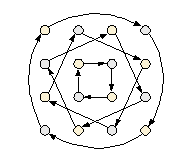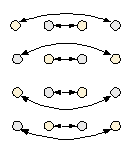sv симметрия относительно вертикальной оси

Поэтому общее число магических квадратов кратно 8 и достаточно найти по одному представителю для каждого класса из K₄.

3.1.2. Группы квадратов (местоположение числа F).

Преобразования ₉₀, _sv и их производные разбивают множество клеток квадрата на 3 группы:

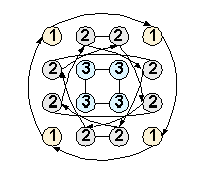
Поэтому множество квадратов разбивается на три попарно непересекающиеся группы в зависимости от того, в какой группе клеток находится максимальное число F₁₆. Таким образом можно рассматривать три вида магических квадратов:

Каждый магический квадрат группы 2 с помощью преобразований ₉₀, _sv и их производных порождает 8 магических квадратов, то есть класс из K₄, причём разные магические квадраты группы 2 порождают разные классы. Что же касается групп 1 и 3, то здесь каждый класс из K₄ порождается двумя разными магическими квадратами, так как группы клеток 1 и 3 содержат не по 8, а по 4 клетки и порождаемый квадрат может быть получен из одного квадрата группы 1 или 3 с помощью поворотов на 90^o: ₉₀, ₉₀², ₉₀³, а из другого - с помощью симметрии и поворотов на 90^o: _sv , _sv90, _sv90².

Поэтому, если n₁, n₂, n₃ - число квадратов в группах 1,2,3, то порождаемые этими группами множества классов K₄₁, K₄₂, K₄₃ (их объединение есть K) содержат, соответственно n₁/2, n₂, n₃/2 классов.

3.1.3. Базовые элементы квадрата и вычисление производных.

Магический квадрат полностью определяется заданием 7 базовых чисел b_i в нём по схеме:

Остальные числа вычисляются по условиям магичности квадрата (x_ij - число в строке i, столбце j):

x₀₃=1E-x₀₀-x₀₁-x₀₂ (строка 0)
x₃₃=1E-x₀₀-x₁₁-x₂₂ (главная диагональ)
x₃₀=1E-x₀₀-x₀₃-x₃₃ (угловые клетки)
x₃₂=1E-x₀₂-x₁₂-x₂₂ (столбец 2)
x₂₁=1E-x₁₁-x₁₂-x₂₂ (центральные клетки)
x₃₁=1E-x₀₁-x₁₁-x₂₁ (столбец 1)
x₁₃=1E-x₁₀-x₁₁-x₁₂ (строка 1)
x₂₀=1E-x₀₀-x₁₀-x₃₀ (столбец 0)
x₂₃=1E-x₂₀-x₂₁-x₂₂ (строка 2)

3.1.4. Магические подквадраты.

В предыдущем пункте я использовал следующие два свойства любого магического квадрата:

• сумма чисел в угловых клетках равна магической сумме:
  a=x 400 0+x 403 0+x 430 0+x 433 0=1E
• сумма чисел в центральных клетках равна магической сумме:
  d=x 411 0+x 412 0+x 421 0+x 422 0=1E

Есть и ещё два свойства:

• сумма чисел в "вертикально-средних" клетках равна магической сумме:
  b=x 401 0+x 402 0+x 431 0+x 432 0=1E
• сумма чисел в "горизонтально-средних"клетках равна магической сумме:
  c=x 410 0+x 420 0+x 413 0+x 423 0=1E

a  b  a c d c a  b  a

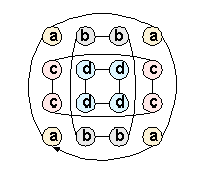Здесь x=a,b,c,d означает сумму всех чисел в клетках, помеченных буквой x

Докажем это:

s - магическая сумма (1E16)
a+b=2s (строки 0+3)	d+b=2s (столбцы 1+2)
a+c=2s (столбцы 0+3)	d+c=2s (строки 1+2)
Отсюда: 2a+(b+c)=4s, 2d+(b+c)=4s; поэтому 2a=2d и a=d
Для диагоналей: a+d=2s; поэтому 2a=2d=2s
Следовательно: a=d=s и значит b=s, c=s

3.1.5. Последовательность вычислений производных элементов.

Последовательность вычислений x_ij в п.3.1.3 дана такой, чтобы раньше "ловилась" немагичность квадрата при данном наборе базовых чисел b_i: как только получится x_ij<0 или x_ij>E или x_ij совпадает с одним из уже использованных чисел, можно переходить к следующему набору b_i.

3.2. Результаты, выданные компьютером.

Центрально-симметричным квадратом назовём квадрат, в котором сумма чисел в центрально-симметричных клетках квадрата равна половине магической суммы - F₁₆/2.

Компьютер дал следующие результаты:

Отсюда следует:

Нумерологически числа, выданные компьютером, весьма значимы:

1296 = 18 * 72 = (2 * 3 52 0) * (2 53 0 * 3 52 0) = 2 54 0 * 3 54 0 = 6 54 0 = 3 * 432
416 = 432 - 16 = 32 * 13 = 2 55 0 * 13 = 2 54 0 * 26
464 = 432 + 32 = 16 * 29 = 2 54 0 * 29
1296 = 416 + 464 + 416 = 2 54 0*26 + 2 54 0*29 + 2 54 0*26 = 2 54 0*(26+29+26)
72 = 2 * 36 = 3 * 24 = 4 * 18 = 6 * 12 = 8 * 9 = 5 02 53 0 * 3 52
24 = 2 * 12 = 3 * 8 = 4 * 6 = 5 02 53 0 * 3

Представляется весьма интересным, что число квадратов группы 2 больше числа квадратов в группе 1 или 3, в то время как число центрально-симметричных квадратов всех групп одинаковое.

3.3. Преобразования множеств классов K₄₁ и K₄₃ друг в друга.

Множества классов K₄₁ и K₄₃ преобразуются друг в друга с помощью преобразования:

13	F	При этом ряды переходят друг в друга так:
		строка 1 строка 0 строка 0 строка 1 строка 3 строка 2 строка 2 строка 3	столбец 1 столбец 0 столбец 0 столбец 1 столбец 3 столбец 2 столбец 2 столбец 3
		Диагонали остаются на месте.

Преобразование ₁₃, правда, переводит число F из клетки [0,0] (группа 1) не в клетку [2,2] (группа 3), а в клетку [1,1], то есть магический квадрат переходит не в главного представителя класса. Для точного преобразования нужно ещё выполнить поворот на 180_o (два поворота на 90_o). Полная схема:

13*90*90

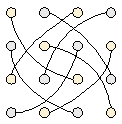Это преобразование сохраняет центральную симметрию: центрально-симметричные клетки квадрата переходят в центрально-симметричные клетки. Поэтому это преобразование переводит друг в друга два множества S₄₁S₄₃.

3.4. Преобразования множеств классов S₄₁S₄₂ и S₄₂S₄₃.

Существуют преобразования S₄₁S₄₂ и S₄₂S₄₃. Им соответствуют схемы:

12	-   -               -   -               -   -               -   -		Ряды переходят друг в друга так: строки остаются на месте, столбцы меняются местами 01 и 23		|   |   |   |                           |   |   |   |	23
			Ряды переходят друг в друга так: столбцы остаются на месте, строки меняются местами 01 и 23

Что же касается диагоналей, то в них (из них) переходят четвёрки чисел из "диагональных" прямоугольников:

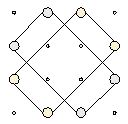Каждый из этих прямоугольников состоит из двух пар центрально-симметричных клеток. Поскольку сумма чисел в клетках каждой такой пары равна половине магической суммы, сумма чисел в таком прямоугольнике равна магической сумме.

Преобразования ₁₂ и ₂₃ как и в п.3.3 переводят магический квадрат не в главного представителя класса. Для точного преобразования в случае ₁₂ нужно ещё симметричное преобразование относительно вертикальной оси _sv, а в случае ₂₃ - поворот на 90_o - ₉₀ . Полные схемы:

12*sv

23*90

3.5. Кое-что о булевых алгебрах.

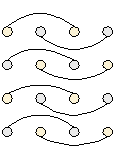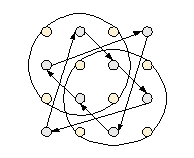Далее я буду рассматривать в основном центрально-симметричные магические квадраты. "Логический" смысл таких квадратов: центрально-симметричные клетки занимают взаимно-инвертированные логические операции: a(x,y) и a(x,y).

Обозначим через B₂ булеву алгебру, определённую на множестве I₂ из двух элементов: 0 - "ложь" и 1 -"истина". Рассматриваемые 16 логических операций являются множеством логических функций от двух переменных F₂:I₂xI₂I₂. Саму эту систему 16 логических функций можно рассматривать как множество I₁₆, на котором определена булева алгебра B₁₆ с естественным определением операций.

Числовой код функции является нормой, поскольку удовлетворяются условия:

• aI₁₆ |a|0;
• aI₁₆ такой, что |a|0;
• a,bI₁₆ таких, что a&b=0 верно |ab|=|a|+|b|.

Таким образом, B₁₆ является нормированной булевой алгеброй (также, впрочем, как и B₂: |0|=0, |1|=1).

Если на множестве числовых кодов функций F₂, рассматриваемом как множество шестнадцатиричных чисел 0F, определить логические операции поразрядно, то, очевидно, получится булева алгебра изоморфная B₁₆. Она, конечно, тоже нормирована, если нормой числа считать само это число. Поэтому с равным успехом можно рассматривать систему 16 логических функций или систему шестнадцатиричных чисел 0F, если логические операции и нормирование понимать так, как было сказано выше.

Можно, в свою очередь, рассматривать систему функций F₁₆:I₁₆I₁₆I₁₆. Однако, число таких функций уже слишком велико: 16^16x16 ("область значений в степени область определения"). Однако, некоторое подмножество F₁₆ меня особо интересует, поскольку оно задаёт некоторую систему естественных преобразований магических квадратов логических функций I₁₆.

3.6. Система преобразований .

В разделе 2 я рассматривал преобразования:

• ₁: d₁(x,y)= d(y,x),
• ₃: d₃(x,y)= d(x,y),
• ₅: d₅(x,y)= d(x,y),
• ₆: d₆(x,y)= d(x,y),
• ₇: d₇(x,y)= d(x,x).

Все они являются частными случаями преобразования :dd вида d(x,y)=d(a(x,y),b(x,y)), где a и b - две логические операции. Множество таких преобразований обозначим .

Важное замечание: Преобразование есть преобразование чисел (или логических функций), а не клеток квадрата. Для числа, находящегося в некоторой клетке квадрата, оно определяет число, которое будет находиться в этой клетке квадрата после преобразования. Преобразование клеток, наоборот, определяет в какую клетку попадёт после преобразования число, находившееся в данной клетке. Схемы преобразований ₁, ₃, ₅, ₆, ₇, которые рисовались в разделе 2, есть схемы преобразования клеток. Поэтому эти схемы соответствуют этим преобразованиям только для квадрата Дюрера. Для других квадратов эти преобразования, если их пытаться рассматривать как преобразования клеток, будут иметь другие схемы.

Систему преобразований можно рассматривать как 16 функций, каждая из которых преобразует пару своих аргументов - логических функций a(x,y),b(x,y) в одну логическую функцию d(a(x,y),b(x,y)). То есть - как множество D из 16 функций d:I₁₆I₁₆I₁₆, то есть DF₁₆. Однако, как преобразования, система рассматривается не как 16 функций от a и b, а наоборот, как 16*16=256 функций от d: при заданных a и b (a,b):I₁₆I₁₆.

Иными словами, система есть множество троек (d,a,b), где d,a,bI₁₆, и это можно интерпретировать как 16 отображений вида I₁₆I₁₆I₁₆ или как 16*16 отображений вида :I₁₆I₁₆. Меня интересует последнее.

С учётом сказанного в п.3.5 об изоморфности 16 логических функций и системы шестнадцатиричных чисел 0F в формуле d=d(a,b) d,d,a,b можно считать либо операциями, либо числами.

3.7. Интерпретации булевой алгебры.

Прежде всего исследуем вопрос о взаимно-однозначности преобразования d=d(a,b). Пример преобразования ₇, преобразующего 16 функций в 4 различные функции (0,1,x,x), показывает, что не все такие преобразования являются взаимно-однозначными. Это значит, что в некоторых случаях результатом преобразования будет квадрат не из 16 разных чисел 0F, а квадрат, заполненный меньшим числом разных чисел так, что некоторые числа 0F встречаются более чем в одной клетке квадрата, а некоторые - не встречаются вовсе. Однако, если в таком квадрате суммы чисел по строкам, столбцам и диагоналям одинаковы, он называется обобщённым магическим квадратом.

Сейчас я проведу рассуждение, быть может, не вполне формальное (но, кстати, легко формализуемое), но зато достаточно наглядное. Это будет рассуждение "в картинках" или, если угодно, "в схемах". Формально это означает, что будут использоваться интерпретации булевой алгебры B₁₆. По отношению к этим интерпретациям булева алгебра B₁₆ есть идеализация (идеализирующая абстракция). Интерпретации, которые я буду использовать, являются тоже абстракциями - репрезентативными абстракциями. Репрезентация даёт возможность подбирать наиболее "наглядную" интерпретацию. Вообще нумерологичность, видимо, тесно связана с "наглядностью". Наглядность же означает некую самоочевидность, которая, в свою очередь, есть некое "автоматическое доказательство", "непосредственное усмотрение" и "прозрачное сведение к аксиомам". Но все эти вопросы, естественно возникающие по ходу дела, я пока откладываю на будущее с тем, чтобы не отвлекаться от изложения фактического материала, связанного с магическими квадратами и логическими функциями.

3.7.1. Алгебра множеств.

3.7.1.1. Картинка логических операций.

В булевой алгебре подмножеств некоторого множества картинка логических операций выглядит так:

d(x,y)

xy   x\y     x&y y\x

x и y - два прямоугольника внутри большого прямоугольника, соответствующего всему множеству (1). Здесь 4 взаимно-непересекающиеся базовые области соответствуют 4-м операциям. Всего операций 16 - каждой операции соответствует область, состоящая из нескольких (от 0 до 4-х) из этих областей: 16=24.

3.7.1.2. Взаимно-однозначность преобразований .

Преобразование d=d(a,b) даёт все 16 разных значений, если a и b - это такие области, которые имеют непустое пересечение, не вложены целиком друг в друга и не составляют в совокупности всё множество. Иными словами, a и b - это такие области, которые ведут себя так же, как области x и y на картинке выше.

d(a,b)

ab   a\b     a&b b\a

a\b, a&b, b\a, ab

3.7.1.3. Число разных значений преобразований .

Если одна из областей a&b, a\b, b\a, ab пуста, то, очевидно, число базовых областей будет меньше и, значит, меньше будет разных значений d(a,b) (объединений этих базовых областей). Все эти 4 области, очевидно, пусты быть не могут, поскольку их объединение - это всё множество (а оно непусто).

В зависимости от числа пустых базовых областей будет то или иное число разных значений d(a,b):

Наши 4 базовые области - это 4 базовые логические операции: a&b, a\b, b\a, ab. Ясно, что тождественность одной из них 0 означает, что d(a,b) даёт тождественный 0 при d равной соответствующей базовой операции.

3.7.1.4. Алгебра подматриц матрицы 2x2.

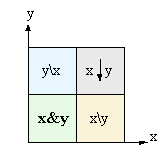	Можно выбрать более чёткую интерпретацию множеств. Рассмотрим квадрат 2x2. 4 его клетки - это 4 базовые области; x - это две клетки нижней строки, y - это две клетки левого столбца.
0 1 2 3 0 1 2 3	В этой интерпретации исходный магический квадрат (Дюрера) логических функций d(x,y) можно нарисовать в следующем виде (зачернённые клетки показывают соответствующие области).

3.7.2. Алгебра элементов тетраэдра.

3.7.2.1. Элементы тетраэдра как логические функции.

Другая интерпретация - представление системы из 16 логических функций в виде тетраэдра:

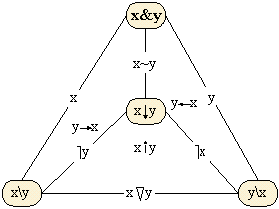xy - невидимая грань 16 элементов тетраэдра: 4 вершины 6 рёбер 4 грани 0 - пустое множество 1 - весь тетраэдр (объём внутри него)

3.7.2.2. Логические операции над элементами тетраэдра.

Как выглядят на тетраэдре логические операции? Дадим их интерпретацию для трёх операций, через которые выражаются все остальные:

• Конъюнкция (&) элементов тетраэдра - это их пересечение (общая часть).
• Дизъюнкция () элементов тетраэдра - это порождение ими другого элемента по схеме:
  • две вершины - ребро между ними
  • два ребра - их общая грань или (если они не лежат на одной грани) весь тетраэдр
  • две грани - весь тетраэдр
  • вершина и ребро - грань, которой они принадлежат, или (если вершина часть ребра) это ребро
  • вершина и грань - весь тетраэдр или (если вершина лежит на этой грани) эта грань
  • ребро и грань - весь тетраэдр или (если ребро лежит на этой грани) эта грань
  • пустое множество и элемент - этот элемент
  • весь тетраэдр и элемент - весь тетраэдр
• Отрицание () элементов тетраэдра:
  • вершина - противоположная грань
  • ребро - противоположное ребро
  • грань - противоположная вершина
  • пустое множество - весь тетраэдр
  • весь тетраэдр - пустое множество

3.7.2.3. Число преобразований разных типов.

Посмотрим в этой интерпретации число преобразований d=d(a,b) разных типов.

Обозначения:

• В - вершина,
• Р - ребро,
• Г - грань,
• Т - весь тетраэдр,
• - пустое множество,
• - непустое множество.
• a = b - a и b совпадают
• a b - a отлично от b
• a = b - a противоположно b:
  • вершина и противолежащая грань,
  • грань и противолежащая вершина,
  • ребро и несмежное с ним ребро)
• a b - a есть часть b
• a b - a не есть часть b
• a b - b есть часть a
• a b - b не есть часть a

число значений - число разных значений, которые принимает функция d(a,b).
число функций - число соответствующих функций d(a,b).

a   b a&b a\b= a&b b\a= a&b ab= a&b число значений число функций   2 1 4*1 = 4   Т Т   Т   Т Т   (ВРГ)     4 4+6+4 = 14 6*14 = 84 (ВРГ)   Т       (ВРГ)     (ВРГ)       (ВРГ) = (ВРГ)     (ВРГ) = (ВРГ)     В Р 8 4*3 = 12 12*12 = 144 Р В 6*2 = 12 В Р 4*3 = 12 В Г Р Г 6*2 = 12 Г В 4*3 = 12 Г Р Р В 6*2 = 12 Г Г 4*3 = 12 Г Р Р Г 6*2 = 12 Р Р Р 16 6*4 = 24 24 Итого: 256

3.8. Центрально-симметричные квадраты

3.8.1. Магические четвёрки чисел.

В п.3.1.4 были указаны 4 четвёрки клеток, сумма чисел в каждой из которых равна магической сумме, если квадрат магический. Для центрально-симметричных магических квадратов в п.3.4 были указаны ещё две четвёрки. На самом деле, в центрально-симметричных квадратах даже независимо от их магичности таких четвёрок 28.

В самом деле, центральная симметрия квадрата разбивает всё множество клеток на 2 класса по 8 клеток (например, строки 0,1 и строки 2,3) таких, что для каждой клетки одного класса центрально-симметричная ей клетка находится в другом классе. Для построения четвёрки достаточно выбрать 2 клетки одного класса и добавить к ним 2 центрально-симметричные им клетки из другого класса. Поскольку такая четвёрка содержит две пары чисел таких, что сумма чисел в каждой паре равна половине магической суммы (это условие центрально-симметричности квадрата), то сумма всех чисел четвёрки равна магической сумме. 2 клетки из 8 можно выбрать C₈² способами:

C82 =	8!	= 28
	2!6!

3.8.2. Число центрально-симметричных квадратов.

Можно подсчитать общее число центрально-симметричных квадратов. Такой квадрат однозначно определяется расположением в его клетках первых 8 чисел (07), поскольку для каждого 0x7 выполняется 8F-xF. Число способов расположения 8 чисел в 16 клетках равно:

A168 =	16!	= 9*10*11*13*14*15*16 = 518.918.400
	8!

Пример центрально-симметричного квадрата, не являющегося магическим, - естественное расположение чисел по строкам в порядке возрастания:

для десятичных чисел

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16

0   1   2   3  4 5 6 7 8 9 A B C D E F

для шестнадцатиричных чисел

Пересечение множеств центрально-симметричных квадратов и магических квадратов содержит, как указано в п.3.2, 384 квадрата (или 384/8=48 классов S₄).

3.9. Преобразования и размещения с повторениями.

Для дальнейших исследований преобразования d=d(a,b) я хочу использовать следующую интерпретацию этого преобразования.

Обозначение: x|r - значение двоичного разряда r числа x, где x=0F, а r=3,2,1,0.

Итак, d(x,y) = d(a(x,y),b(x,y)). Согласно таблице логических функций в п.2.1:

• 3-ий разряд числового кода логической функции соответствует значениям аргументов x=0,y=0; поэтому: a|r=0, b|r=0 d|r=d|3.
• 2-ой разряд числового кода логической функции соответствует значениям аргументов x=0,y=1; поэтому: a|r=0, b|r=1 d|r=d|2.
• 1-ый разряд числового кода логической функции соответствует значениям аргументов x=1,y=0; поэтому: a|r=1, b|r=0 d|r=d|1.
• 0-ой разряд числового кода логической функции соответствует значениям аргументов x=1,y=1; поэтому: a|r=1, b|r=1 d|r=d|0.

В целом получается: d|r=d|(3-2(a|r)-b|r). Иными словами, r-ый разряд числового кода d(x,y) есть q-ый разряд числового кода d(x,y), где q=3-2(a|r)-b|r.

Таким образом, числовой код d(x,y) получается из числового кода d(x,y) с помощью размещения с повторениями значений 4-х разрядов числового кода d(x,y) по 4-м разрядам числового кода d(x,y).

Число размещений с повторениями из n элементов по m позициям равно n^m. В данном случае это 4⁴=256 - число всех преобразований из , которое в п.3.6 вычислялось как 16² (число разных значений аргумента a, умноженное на число разных значений аргумента b):

4⁴=256=16².

Можно по-другому вычислить и число разных типов (смотри п.3.7.2.3): p - число пустых базовых областей - это число разрядов числового кода d, не участвующих в размещении. Поэтому число разных значений, которые принимает функция d, равно 2^4-p: 16,8,4,2.

Обозначения:

• R_n^m - число размещений всех n элементов по m позициям (nm), то есть каждый элемент участвует в размещении;
• C_n^m - число сочетаний из n по m;
• P^m - число перестановок m элементов.

Pm = m!

n! Cnm =    m!(n-m)!

R1m = 1

Rmm = Pm

Rnm =	nRnm-1	+	nRn-1m-1	= n(Rnm-1+Rn-1m-1)
			число размещений, когда в 1-ой позиции находится элемент, не повторяющийся в других m-1 позициях
	число размещений, когда в 1-ой позиции находится элемент, повторяющийся в других m-1 позициях

Число преобразований для данного p:

• p=0 - R₄⁴ = P⁴ = 4! = 24
• p=1 - C₄¹*R_4-1⁴ = C₄¹*R₃⁴ = C₄¹*R_4-1⁴ = C₄¹*3(R₃³+R₂³) = C₄¹*3(P³ + 2(R₂²+R₁²)) = C₄¹*3(P³+2(P²+1)) = 4*3(6+2(2+1)) = 144
• p=2 - C₄²*R_4-2⁴ = C₄²*R₂⁴ = C₄²*2(R₂³+R₁³) = C₄²*2(2(R₂²+R₁²)+R₁³)) = C₄²*2(2(P²+1)+1)) = 6*2(2(2+1)+1) = 84
• p=3 - C₄³*R_4-3⁴ = C₄³*R₁⁴ = C₄³*1 = 4*1 = 4

3.10. Перестановочные преобразования.

3.10.1. Группа перестановочных преобразований.

Преобразование является взаимно-однозначным только при p=0. В этом случае преобразование порождается некоторой перестановкой 4-х разрядов числового кода логической функции d. Верно и обратное: каждая перестановка разрядов числового кода функции d порождает некоторое преобразование из . Такие преобразования назовём перестановочными преобразованиями, а множество перестановочных преобразований обозначим P.

Если умножение преобразований определять естественным образом: a()=(a), то P изоморфно группе перестановок 4-х элементов, называемой обычно группой подстановок 4-й степени или симметрической группой степени 4.

3.10.2. Сохранение центральной симметрии.

Любое преобразование P сохраняет центральную симметрию квадрата. Действительно, если a и b находятся в центрально-симметричных клетках, то по условию центрально-симметричности квадрата a=F-b. Поразрядно это выглядит так:

a|3 = (b|3)

a|2 = (b|2)

a|1 = (b|1)

a|0 = (b|0)

то есть в соответствующих разрядах a и b находятся противоположные коды (0-1 или 1-0). Ясно, что любая перестановка разрядов, применяемая одновременно к a и к b, сохраняет это свойство.

3.10.3. Система образующих.

Как известно, у группы подстановок n-ой степени есть система образующих из двух элементов: транспозиция двух элементов и циклическая перестановка всех n элементов. То есть каждую подстановку можно представить как произведение нескольких образующих элементов. В качестве транспозиции и циклической перестановки можно выбрать любую транспозицию и любую циклическую перестановку всех элементов, например:

	1,2,3,...,n-1,n			1,2,3,...,n-1,n
	1,2,3,...,n,n-1			n,1,2,...,n-2,n-1

Если верхний ряд элементов это 1,2,3,...,n-1,n, его обычно не записывают и пишут просто:

(1,2,3,...,n,n-1)      (n,1,2,...,n-2,n-1)

Для наших целей, когда элементы - это разряды двоичного числового кода логической функции, подразумеваемый верхний ряд будет (3,2,1,0). Я выбираю следующую систему образующих:

0 = (3,2,1,0) =		3,2,1,0			1 = (2,1,0,3) =		3,2,1,0
		3,2,0,1					2,1,0,3

Мы не будем специально отличать подстановку 4-ой степени и порождаемое ею преобразование из P, если это не приводит к путанице и по контексту можно понять, что имеется в виду.

Найдём a₀, b₀ и a₁, b₁ для выражений (a₀,b₀)=₀ и (a₁,b₁)=₁, используя равенство из п.3.9 d|r=d|(3-2(a|r)-b|r)

3-2(a0|0)-b0|0=1 a0|0=1, b0|0=0		3-2(a1|0)-b1|0=3 a1|0=0, b1|0=0
3-2(a0|1)-b0|1=0 a0|1=1, b0|1=1		3-2(a1|1)-b1|1=0 a1|1=1, b1|1=1
3-2(a0|2)-b0|2=2 a0|2=0, b0|2=1		3-2(a1|2)-b1|2=1 a1|2=1, b1|2=0
3-2(a0|3)-b0|3=3 a0|3=0, b0|3=0		3-2(a1|3)-b1|3=2 a1|3=0, b1|3=1

Поэтому:

a₀ = 8(a₀|3)+4(a₀|2)+2(a₀|1)+a₀|0 = 8*0+4*0+2*1+1 = 3
b₀ = 8(b₀|3)+4(b₀|2)+2(b₀|1)+b₀|0 = 8*0+4*1+2*1+0 = 6

a₁ = 8(a₁|3)+4(a₁|2)+2(a₁|1)+a₁|0 = 8*0+4*1+2*1+0 = 6
b₁ = 8(b₁|3)+4(b₁|2)+2(b₁|1)+b₁|0 = 8*1+4*0+2*1+0 = A

₀ = (3,2,0,1) = d(3,6) = d(x,xy)
₁ = (2,1,0,3) = d(6,A) = d(xy, y)

Все остальные перестановочные преобразования получаются из этих двух с помощью умножения (то есть последовательного выполнения) преобразований.

3.10.4. Преобразование клеток и преобразование чисел.

В п.3.6 было важное замечание о преобразованиях чисел и преобразованиях клеток квадрата. На самом деле эти преобразования связаны между собой.

Квадрат k до сих пор мы рассматривали как матрицу 4x4 элементов, каждый из которых есть число 0F. Элемент в клетке [i,j] (строка i, столбец j) матрицы обозначим k[i,j].

Вместе с тем квадрат k можно рассматривать и как вектор из 16 элементов, каждый из которых есть число 0F. h-ый элемент вектора обозначим k[h].

Квадрат как вектор можно рассматривать как взаимно-однозначное преобразование индексов - преобразование вида I₁₆I₁₆. В этом случае для iI₁₆ и квадрата k число k[i] будем записывать, как это принято для преобразований, в виде ik.

Преобразование клеток квадрата есть преобразование индексов клеток. Это значит, что любое преобразование (и вообще любое взаимно-однозначное преобразование множества I₁₆) можно применять к индексам квадрата-вектора.

Пусть есть квадрат k и взаимно-однозначное преобразование :I₁₆I₁₆. Будем применять преобразование как преобразование клеток квадрата k. В результате такого преобразования мы получим преобразование чисел квадрата k. Для каждого iI₁₆ число ik из клетки i переходит в клетку i. Именно это изображается стрелкой на схеме преобразования клеток. С другой стороны, до преобразования в клетке i находилось число (i)k. Поэтому для каждого iI₁₆ ((i)k) = ik. То есть k = k. Отсюда: k = k^-1, = k^-1k^-1.

Таким образом, каждому преобразованию чисел соответствует некоторое преобразование клеток , и наоборот, но это соответствие зависит от квадрата k. Именно поэтому схемы преобразований клеток, которые рисовались в разделе 2, соответствуют преобразованиям чисел, задаваемым формулами ₁, ₃, ₅, ₆, ₇, только для квадрата Дюрера. Для других квадратов эти преобразования, если их пытаться рассматривать как преобразования клеток, будут иметь другие схемы.

3.10.5. Магичность преобразований .

Теперь рассмотрим вопрос о магичности квадрата, получающегося из магического квадрата в результате преобразования d(a,b).

Прежде всего следует сказать, что, если магический квадрат d(x,y) - не является центрально-симметричным, то квадрат d(x,y) = d(a(x,y),b(x,y)) может оказаться не магическим. Для этого достаточно привести пример:

F D 0 2 4 1 E B 3 6 9 C 8 A 7 5	d(5,6) = d(y,xy) переводит магический квадрат в немагический квадрат	F E 0 1 2 4 B D 5 3 C A 8 9 7 6

Я намеревался доказать магичность (сохранение магичности) преобразований из P для центрально-симметричных магических квадратов. Для этого достаточно было бы доказать магичность двух преобразований ₀ и ₁, составляющих систему образующих P. Если бы ₀ и ₁ были преобразованиями клеток, это было бы легко доказать. Но это преобразования чисел, а соответствующие им преобразования клеток - свои для каждого квадрата k. Так что такая попытка доказательства оказалась неудачной. Другое доказательство будет дано позже.

3.10.6. Структура группы перестановочных преобразований.

Рассмотрим группу преобразований P. Это преобразования вида d = d(a,b), где a,bI₁₆ и выполняются условия a&b0, a\b0, b\a0, ab0. Эта группа содержит 24 преобразования, каждое и которых переводит центрально-симметричный магический квадрат в центрально-симметричный магический квадрат (хотя это ещё не доказано) и оставляет на месте числа 0 ("тождественная ложь") и F ("тождественная истина"). Если выбран некоторый центрально-симметричный магический квадрат d (например, квадрат Дюрера), то с помощью этих 24 преобразований из него получаются ещё 23 квадрата, поскольку одно из преобразований группы P - тождественное. Всего - 24 квадрата. Поскольку число F может занимать любую из 16 клеток, а положение числа 0 однозначно определяется положением числа F (0 находится в клетке центрально-симметричной клетке числа F), всего получаем 16*24=384 центрально-симметричных магических квадратов. Это согласуется с данными компьютера в п.3.2.

В разложении на преобразования ₀ и ₁ группа P выглядит так:

Структура

Горизонтальные линии соответствуют преобразованию ₁.
Вертикальные и диагональные линии соответствуют преобразованию ₀.
- тождественное преобразование.

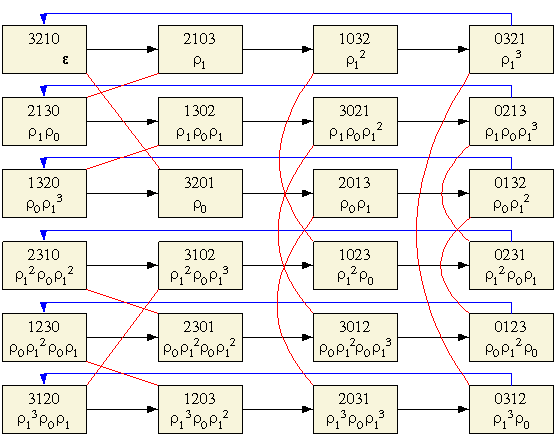
Соответствующие преобразования в структуре можно записать в таблице:

	1	12	13
1  0	1  01	1  012	1  013
013	0	01	012
12012	12013	120	1201
01201	012012	012013	0120
1301	13012	13013	130

3.11. Система преобразований .

В разделе 2 я рассматривал также преобразования:

₂: d₂(x,y) = d(x,y),
₄: d₄(x,y) = d(x,y).

Все они являются частными случаями преобразования, которое можно рассматривать как логическую операцию, одним из операндов которой является преобразование . Формально это записывается: a(b(x,y),d(a₁(x,y),b₁(x,y)), где a,b,a₁,b₁ - логические операции. Иначе можно записать: a(b(x,y), d(x,y)), где и = (a₁,b₁). Такое преобразование есть произведение (последовательное выполнение) преобразования и преобразования вида d = a(b,d), то есть каждый элемент квадрата d получается в результате выполнения логической операции a, первым операндом которой является логическая операция b, а вторым - соответствующий элемент (логическая операция) квадрата d.

Множество таких преобразований обозначим .

Важное замечание: Преобразование , также как преобразования , есть преобразование чисел (или логических функций), а не клеток квадрата.

3.12. Условие взаимно-однозначности преобразований .

Исследуем вопрос о взаимно-однозначности преобразований . Прежде всего, посмотрим как устроены сами логические функции d(x,y), точнее, их числовые коды. Как и в п.3.9 обозначим x|r - значение двоичного разряда r числа x. Для x=0F r=3,2,1,0.

d = 8(d|3)+4(d|2)+2(d|1)+1(d|0)

Поэтому:

d(x,y) = 8(x,y)&(d|3)+4(x,y)&(d|2)+2(x,y)&(d|1)+1(x,y)&d|0
d(x,y) = (xy)&(d|3)+ (y\x)&(d|2)+ (x\y)&(d|1)+ (x&y)&d|0

Заметим, что 8,4,2,1, то есть (xy), (y\x), (x\y), (x&y), - это те четыре базовые области, о которых шла речь в п.3.7.

Также как в п.3.9, можно записать:

d(x,y)|r = d|(3-2(x|r)-y|r)

Поэтому для d=a(b,d):

(d)|r = a|(3-2(b|r)-d|r)

Таким образом, i-ый разряд d есть j-ый разряд a, где j=3-2(b|r)-d|r

Иначе можно записать:

(d)|r = a|(3-2(b|r)), если d|r=0
(d)|r = a|(2-2(b|r)), если d|r=1

Для того, чтобы преобразование для d=0F давало все 16 разных чисел, нужно чтобы:

r=0,1,2,3 a|(3-2(b|r)) a|(2-2(b|r))

То есть: r=0,1,2,3 (b|r=0)(a|3 7- 0a|2) и (b|r=1)(a|1 7- 0a|0)

Здесь получаются 3 случая:

1. b=0.	Тогда a|3a|2 и (d1)|r = a|(3-d|r) =		a|3, если d|r=0
			a|2, если d|r=1
2. b=F.	Тогда a|1a|0 и (d2)|r = a|(1-d|r) =		a|1, если d|r=0
			a|0, если d|r=1
3. b0 и bF.	Тогда a|3a|2, a|1a|0 и (d3)|r =		a|(3-2(b|r)), если d|r=0	=		a|3, если b|r=0 и d|r=0
						a|1, если b|r=1 и d|r=0
			a|(2-2(b|r)), если d|r=1			a|2, если b|r=0 и d|r=1
						a|0, если b|r=1 и d|r=1

Поэтому:

(a|3=0,a|2=1) d₁₁ = 4(0,d) = 5(0,d) = 6(0,d) = 7(0,d) = d
(a|3=1,a|2=0) d₁₂ = 8(0,d) = 9(0,d) = A(0,d) = B(0,d) = d
(a|1=0,a|0=1) d₂₁ = 1(1,d) = 5(1,d) = 9(1,d) = D(1,d) = d
(a|1=1,a|0=0) d₂₂ = 2(1,d) = 6(1,d) = A(1,d) = B(1,d) = d

(a|3=0,a|2=1 и a|1=0,a|0=1) d₃₁ = 5(b,d) = d
(a|3=0,a|2=1 и a|1=1,a|0=0) d₃₂ = 6(b,d) = bd
(a|3=1,a|2=0 и a|1=0,a|0=1) d₃₃ = 9(b,d) = bd
(a|3=1,a|2=0 и a|1=1,a|0=0) d₃₄ = A(b,d) = d

Заметим, что bd = bd и bd = bd.

Таким образом, взаимно-однозначными являются следующие преобразования:

0 = 0d = Fd = d		8 = 8d = 7d
1 = 1d = Ed		9 = 9d = 6d
2 = 2d = Dd		A = Ad = 5d
3 = 3d = Cd		B = Bd = 4d
4 = 4d = Bd		C = Cd = 3d
5 = 5d = Ad		D = Dd = 2d
6 = 6d = 9d		E = Ed = 1d
7 = 7d = 8d		F = Fd = 0d = d

Общий вид преобразования : d = bd = bd, где bI₁₆.

Преобразование инвертирует некоторые разряды d, а именно те, которые определяются параметром b. Такое преобразование назовём инвертирующим, а множество инвертирующих преобразований обозначим T.

3.13. Инвертирующие преобразования.

3.13.1. Группа инвертирующих преобразований.

Множество преобразований T является группой преобразований по операции умножения (последовательного выполнения) преобразований. Это утверждение очевидно следует из свойств исключающей дизъюнкции:

b1(b2d) = (b1b1)d	- произведение инвертирующих преобразований есть инвертирующее преобразование
b(bd) = d	- преобразование, обратное инвертирующему, тоже есть инвертирующее преобразование

Заметим, что любое инвертирующее преобразование обратно самому себе: T =, то есть ^-1 = .

3.13.2. Сохранение центральной симметрии.

Любое преобразование T сохраняет центральную симметрию квадрата. Действительно, если d₁ и d₂ находятся в центрально-симметричных клетках, то по условию центрально-симметричности квадрата d₁ = d₂. После преобразования (bd₁) = (bd₂) = bd₂ = (bd₂).

3.13.3. Система образующих.

Заметим, что если b&c=0, то (bc)d=c(bd).

Действительно:
c(bd)
= c&(bd)c&(bd)
= c&(bd)c&(bd)
= c&(b&db&d)c&(b&db&d)
= c&b&dc&b&dc&b&dc&b&d
= 0&d(c&bc&b)&dc&b&d
= ((c&b)&(c&b))&dc&b&d
= ((cb)&(cb))&dc&b&d
= (c&cc&bb&cb&b)&dc&b&d
= (0c&b00)&dc&b&d
= (c&b)&dc&b&d
= (cb)&dc&b&d
= (cb)&d(cb)&d
= (cb)d
= (bc)d

Любое число bI₁₆ и b0 может быть выражено как поразрядная дизъюнкция чисел 1,2,4,8. Учитывая, что инвертирующее преобразование обратно самому себе, получаем систему образующих группы инвертирующих преобразований, состоящую из 4-х преобразований ₁, ₂, ₄, ₈:

0 = 1 1	4 = 4	8 = 8	C = 8 4
1 = 1	5 = 4 1	9 = 8 1	D = 8 4 1
2 = 2	6 = 4 2	A = 8 2	E = 8 4 2
3 = 2 1	7 = 4 2 1	B = 8 2 1	F = 8 4 2 1

Вот эти четыре образующие инвертирующие преобразования:

d₁(x,y) = (1d)(x,y) = 1(x,y)d(x,y) = (x&y)d(x,y)
d₂(x,y) = (2d)(x,y) = 2(x,y)d(x,y) = (x\y)d(x,y)
d₄(x,y) = (4d)(x,y) = 4(x,y)d(x,y) = (y\x)d(x,y)
d₈(x,y) = (8d)(x,y) = 8(x,y)d(x,y) = (xy)d(x,y)

Как видно, они соответствуют 4-м базовым областям, о которых шла речь в п.3.7.

3.13.4. Магичность преобразований T.

Прежде всего, покажем, что для квадратов без центральной симметрии магичность может и не сохраняться. Пример - тот же, что и в п.3.10.5:

F D 0 2 4 1 E B 3 6 9 C 8 A 7 5	(1d)(x,y)=(x&y)d(x,y) переводит магический квадрат в немагический квадрат	E C 1 3 5 0 F A 2 7 8 D 9 B 6 4

Доказательство магичности преобразований из T для центрально-симметричных магических квадратов будет дано позже.

3.13.5. Структура группы инвертирующих преобразований.

Рассмотрим группу преобразований T. Это преобразования вида d=td(a,b), где tI₁₆. Эта группа содержит 16 преобразований, каждое из которых переводит центрально-симметричный магический квадрат в центрально-симметричный магический квадрат (хотя это ещё не доказано), и, если оно нетождественно, перемещает числа 0 ("тождественная ложь") и F ("тождественная истина"). Если выбран некоторый центрально-симметричный магический квадрат d (например, квадрат Дюрера), то с помощью этих 16 преобразований из него получаются ещё 15 квадратов, поскольку одно из преобразований группы T - тождественное. Всего - 16 квадратов, причём число F во всех этих квадратах занимает разные позиции, а положение числа 0 однозначно определяется положением числа F (0 находится в клетке центрально-симметричной клетке числа F). Каждый из этих 16 квадратов с помощью преобразований P порождает ещё 23 квадрата (п.3.10.6). Поэтому всего получаем 16*24=384 центрально-симметричных магических квадрата. Это согласуется с данными компьютера в п.3.2.

В разложении на преобразования ₁, ₂, ₄, ₈ группа T образует структуру четырёхмерного куба. 4-хмерный куб можно представить в виде двух 3-хмерных кубов, вложенных один в другой, а 3-хмерный куб - в виде двух квадратов, вложенных один в другой. В целом получаются 4 иерархично вложенных квадрата:

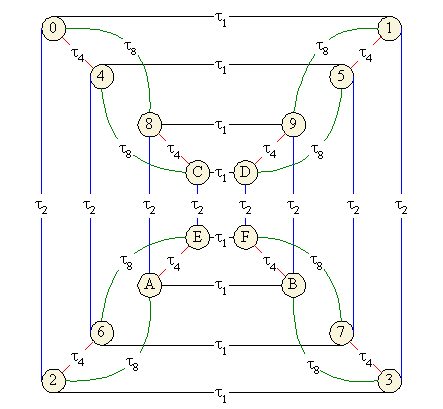
4-хмерный куб топологически эквивалентен тору: если в представлении 4-хмерного куба как вложенных один в другой двух 3-хмерных кубов внутренность внутреннего куба рассматривать как "дырку от бублика", то как раз получится тор. Эту структуру можно представить также в следующем виде: