4. ТЕОРИЯ МАГИЧЕСКИХ КВАДРАТОВ 4-ГО ПОРЯДКА.

1. Числа.
2. Преобразования.
   1. Инвертирующие преобразования.
   2. Перестановочные преобразования.
   3. Логические преобразования.
3. Квадраты.
   1. Магичность.
   2. Равномерность.
   3. Симметричность.
   4. Пять типов квадратов 4-го порядка.
4. Квадраты и преобразования.
   1. Преобразование чисел как преобразование квадратов.
   2. Квадраты как преобразования. Умножение.
   3. Преобразование клеток квадрата.
   4. Связь преобразований чисел и клеток квадрата.
   5. Логические преобразования чисел квадрата.
   6. Логические преобразования клеток квадрата.
   7. Симметричные магические квадраты.

4.1. Числа.

Как правило под "числом" мы будем иметь в виду неотрицательное целое число.

Обозначение 4.1:1: Для n>0 через I(n) обозначим множество целых чисел от 0 до n-1.

Мы будем рассматривать также двоичное представление числа. Если xI(2^m), то x имеет m двоичных разрядов 0,1,...,m-1.

Обозначение 4.1:2: Для xI(2^m) и rI(m) через x|r обозначим значение r-го двоичного разряда числа x.

	m-1
xI(2m) однозначно раскладывается x =		2r*(x|r)
	r=0

Определение 4.1:1: Для xI(2), то есть x=0,1, его отрицанием называется число x, определяемое следующим образом:

x =		0, если x=1
		1, если x=0

Определение 4.1:2: Для xI(2^m) его отрицанием называется число x, которое есть поразрядное отрицание x, то есть число, в котором значение каждого двоичного разряда есть отрицание значения соответствующего разряда числа x: rI(m) (x)|r = (x|r). Числа x и x будем называть взаимно-инвертированными.

Определение 4.1:3: Для x,yI(2), то есть x,y=0,1, исключающей дизъюнкцией чисел x и y называется число xy, определяемое следующим образом:

xy =		0, если x=y
		1, если xy0

Определение 4.1:4: Для x,yI(2^m) исключающей дизъюнкцией чисел x и y называется число xy, которое есть поразрядная исключающая дизъюнкция x и y, то есть число, в котором значение каждого двоичного разряда есть исключающая дизъюнкция значений соответствующих разрядов чисел x и y: rI(m) (xy)|r = (x|r)(y|r). Число y, фактически, задаёт те двоичные разряды числа x, которые инвертируются при переходе к xy.

Теорема 4.1:1: x,yI(2^m) (x)y = (xy).

Доказательство:

Это утверждение легко проверяются для m=1 (Определения 1,3) и очевидным образом распространяется для поразрядных операций (Определения 2,4).

4.2. Преобразования.

Обозначение 4.2:1: Группу всех взаимно-однозначных преобразований (подстановок) множества I(n) по операции умножения преобразований, определяемой как их последовательное выполнение, иначе называемую группой подстановок, или симметрической группой, степени n, обозначим через (n). Тождественное преобразование (единица группы) будем обозначать .

Обозначение 4.2:2: Подстановку (n) множества I(n) можно записать в виде:

	n-1, n-2, ...,1, 0		или, считая верхний ряд фиксированным:
	(n-1),(n-2),...,1,0		( (n-1),(n-2),...,1,0 )

4.2.1. Инвертирующие преобразования.

Теорема 4.2.1:1: Множество I(2^m) по операции является коммутативной группой со следующими свойствами:

• единицей группы является число 0: aI(2^m) 0a=a;
• каждое число обратно самому себе: a I(2^m) aa=0;
• aI(2^m) a(2^m-1) = a, aa=(2^m-1).

Доказательство:

1. Ассоциативность операции: a,b,cI(2^m) a(bc)=(a b)c.
2. Коммутативность операции: a,bI(2^m) ab=ba.
3. Единицей группы является число 0: aI(2^m) 0a=a;
4. Каждое число обратно самому себе: aI(2^m) aa=0;
5. aI(2^m) a(2^m-1)= a, aa=(2^m-1).

Все эти свойства легко проверяются для m=1 (Определения 4.1:1,3) и очевидным образом распространяется для поразрядных операций (Определения 4.1:2,4).

Обозначение 4.2.1:1: Для tI(2^m) отображение :I(2^m)I(2^m), определяемое xI(2^m) x=xt, будем обозначать (t).

Теорема 4.2.1:2: Если tI(2^m), то отображение (t) является подстановкой множества I(2^m), то есть (t)(2^m).

Доказательство:

Нужно доказать, что отображение (t) является биекцией (взаимно-однозначным отображением) I(2^m) на I(2^m), то есть оно a) инъективно и b) сюръективно.

a) Отображение (t) инъективно, то есть разным x соответствуют разные x(t): x₁,x₂I(2^m) x₁x₂ x₁(t)x₂(t).

Действительно, если x₁x₂, то rI(m) x₁|r x₂|r, поэтому, как непосредственно следует из определения операции , (x₁|r)(t|r) (x₂|r)(t|r) x₁t x₂t, то есть x₁(t) x₂(t).

b) Отображение (t) сюръективно, то есть это отображение I(2^m) на I(2^m), то есть xI(2^m) yI(2^m) такое, что yt()=x.

Действительно, если y=xt, то yt()=yt=(xt)t=x(tt)=x0=x.

Определение 4.2.1:1: Для tI(2^m) преобразование =(t), определяемое xI(2^m) x(t)=xt, назовём инвертирующим порядка 2^m, поскольку определяется инвертированием некоторых двоичных разрядов чисел из I(2^m).

Теорема 4.2.1:3: Число инвертирующих преобразований порядка 2^m равно 2^m.

Доказательство очевидно.

Обозначение 4.2.1:2: Множество инвертирующих преобразований обозначим T(2^m) и для T(2^m) соответствующее число tI(2^m) будем обозначать t=t().

Теорема 4.2.1:4: Множество T(2^m) есть подгруппа группы T(2^m) изоморфная группе I(2^m) по операции.

Доказательство:

Соответствие =(t) можно рассматривать как соответствие I(2^m) и T(2^m). Оно, очевидно:

a) является отображением, то есть каждому tI(2^m) ставит в соответствие только одно (t) в силу определения (t);

b) сюръективно, то есть это отображение I(2^m) на T(2^m) в силу определения T(2^m);

c) инъективно, то есть t₁,t₂I(2^m) t₁t₂ (t₁)(t₂);
действительно, t₁ t₂ 0t₁ 0t₂, то есть 0(t₁) 0(t₂).

Для доказательства изоморфизма нужно показать, что (t₁t₂) = (t₁)(t₂). Действительно, xI(2^m) x(t₁t₂) = x(t₁t₂) = (xt₁)t₂ = (x(t₁))t₂) = (x(t₁))(t₂) = x((t₁)(t₂)).

Теорема 4.2.1:5: Инвертирующее преобразование, обратное данному инвертирующему преобразованию, совпадает с ним самим: T(2^m) ^-1=.

Доказательство:

xI(2^m) x() = (x) = (xt()) = (xt())t() = x(t()t()) = x0 = x. Поэтому ^-1=.

Теорема 4.2.1:6: Подгруппа T(2^m)имеет систему образующих из m преобразований _r = (2^r), где rI(m).

Доказательство:

	m-1
Поскольку tI(2m) можно однозначно представить в виде t =		2r*(x|r)
	r=0

и поскольку операция определена поразрядно, доказательство теоремы очевидно.

4.2.2. Перестановочные преобразования.

Теорема 4.2.2:1: Если {M,} - группа на множестве M с операцией , и на том же множестве M определена операция : x,yM xy=yx, то {M,} будет группой, изоморфной группе {M,}.

Доказательство:

Рассмотрим отображение :MM, ставящее в соответствие каждому элементу его обратный элемент в группе {M,}: xM x=x^-1. Очевидно, что есть взаимно-однозначное отображение M на M. Для доказательства изоморфизма осталось показать, что (xy)=xy. Действительно: (xy)=(yx)=(yx)^-1=x^-1y^-1=xy.

Обозначение 4.2.2:1: Для (m) отображение :I(2^m)I(2^m), определяемое xI(2^m) rI(m) (x)|r=x|(r) будем обозначать ().

Теорема 4.2.2:2: Если (m), то отображение () является подстановкой множества I(2^m), то есть ()(2^m).

Доказательство:

Нужно доказать, что отображение () является биекцией (взаимно-однозначным отображением) I(2^m) на I(2^m), то есть оно a) инъективно и b) сюръективно.

a) Отображение () инъективно, то есть разным x соответствуют разные x(): x₁,x₂I(2^m) x₁x₂ x₁()x₂().

Действительно, если x₁x₂, то rI(m) x₁|rx₂|r. В силу того, что - подстановка множества I(m), r₁I(m) r=r₁ и значит x₁|(r₁)x₂|(r₁), то есть x₁()x₂().

b) Отображение () сюръективно, то есть это отображение I(2^m) на I(2^m), то есть xI(2^m) yI(2^m) такое, что y()=x.

Действительно, если y=x(^-1), то rI(2^m) (y())|r=y|(r)=(x(^-1))|(r)=x|((r)^-1)=x|(r(^-1))=x|r, то есть y() и x совпадают по всем двоичным разрядам и значит x=y().

Определение 4.2.2:1: Для (m) преобразование =(), определяемое xI(2^m) rI(m) (x)|r=x|(r), назовём перестановочным порядка 2^m, поскольку определяется некоторой перестановкой двоичных разрядов чисел из I(2^m).

Теорема 4.2.2:3: Число перестановочных преобразований порядка 2^m равно m!.

Доказательство очевидно.

Обозначение 4.2.2:2: Множество перестановочных преобразований обозначим P(2^m) и для P(2^m) соответствующую подстановку (m) будем обозначать =().

Теорема 4.2.2:4: Множество P(2^m) есть подгруппа группы (2^m) изоморфная группе (m).

Доказательство:

Соответствие =() можно рассматривать как соответствие (m) и P(2^m). Оно, очевидно:

a) является отображением, то есть каждому (m) ставит в соответствие только одно () в силу определения ();

b) сюръективно, то есть это отображение (m) на (2^m) в силу определения P(2^m);

c) инъективно, то есть ₁,₂(m) ₁₂ (₁)(₂); действительно, ₁₂ rI(m) r₁r₂, и значит для x, имеющего "1" в разряде r₁ и "0" в разряде r₂, x|(r₁) x|(r₂), то есть (x(₁))|r (x(₂))|r.

Теперь покажем, что (₁₂)= (₂) (₁). Действительно, xI(2^m) rI(m) (x (₁₂))|r=x|(r(₁₂))=x|((r₁)₂)=(x (₂))|(r₁)=((x (₂)) (₁))|r=(x( (₂) (₁)))|r.

Таким образом, (m) изоморфно P(2^m) с операцией "обратного последовательного выполнения преобразований". В силу теоремы 1 (m) изоморфно также P(2^m) с нормальной операцией "прямого последовательного выполнения преобразований".

Теорема 4.2.2:5: Перестановочное преобразование, обратное данному перестановочному преобразованию, определяется перестановкой двоичных разрядов чисел, обратной перестановке, определяющей данное перестановочное преобразование: P(2^m) (^-1)=(( ))^-1.

Доказательство:

xI(2^m) 2 rI(m) x(()(^-1))|r = ((x())(^-1)|r = (x())|(r^-1) = x|((r^-1)) = x|(r(^-1)) = x|(r) = x|r.

Поэтому ()(^-1)=, то есть ()^-1 = (^-1), то есть (^-1)=(( ))^-1.

Теорема 4.2.2:6: Подгруппа P(2^m) имеет систему образующих из двух элементов: ₀ = (₀) и ₁ = (₁), где

₀ = (m-2,m-1,...,3,2,0,1) - транспозиция чисел 0 и 1
₁ = (m-2,m-3,...,1,0,m-1) - циклический сдвиг всех элементов

Доказательство: Согласно известной теореме теории групп, (m) имеет систему образующих { ₀,₁}. Поскольку (m) изоморфно (2^m), теорема доказана.

4.2.3. Логические преобразования.

Определение 4.2.3:1: Логическим преобразованием порядка 2^m назовём преобразование, которое является преобразованием или произведением нескольких преобразований, каждое из которых - это инвертирующее или перестановочное преобразование порядка 2^m.

Обозначение 4.2.3:1: Множество логических преобразований обозначим (2^m).

Теорема 4.2.3:1: Множество логических преобразований (2^m) является подгруппой группы (2^m).

Доказательство очевидно.

Теорема 4.2.3:2: Группы T(2^m) и P(2^m) имеют единственный общий элемент - тождественное преобразование: T(2^m)P(2^m)=.

Доказательство:

Пусть T(2^m) P(2^m); t=t() =(). Поскольку , t 0 и поэтому t0 ( не изменяет количество "1" в двоичном представлении числа), но t=tt=0. Следовательно, tt и, значит, .

Лемма 4.2.3:1: x,yI(2^m) P(2^m) (xy)=(x)(y).

Доказательство:

Пусть =().

rI(m)	((xy))|r	= (по определению )
=	(xy)|(r)	= (по определению )
=	(x|(r))(y|(r))	= (по определению )
=	((x)|r)((y)|r)	= (по определению )
=	((x)(y))|r.

Следовательно, (xy)=(x)(y), что и требовалось доказать.

Теорема 4.2.3:3: Группа T(2^m) перестановочна с любым преобразованием из P(2^m): P(2^m) T(2^m)= T(2^m). Как следствие подгруппы T(2^m) и P(2^m) перестановочны: T(2^m)P(2^m) = P(2^m)T(2^m).

Доказательство:

Нужно доказать, что P(2^m) T(2^m) ₁,₂T(2^m) такие, что = и = ₂.

Обозначая t=t(), возьмём t₁=t^-1 и, соответственно, ₁=(t₁). Тогда t=t₁ и xI(2^m) x() = (x) = (x)t = (x)(t₁) = (по Лемме 1) = (xt₁) = (x₁) = x(₁). Итак: xI(2^m) x() = x(₁), то есть = ₁. Если теперь t₂ =t, то t=t₂^-1 и для ₂ = (t₂), как только что доказано, ₂ = .

Теорема 4.2.3:4: Подгруппа (2^m), порождённая подгруппами T(2^m) и P(2^m) группы (2^m), совпадает с произведением подгрупп T(2^m)P(2^m)= P(2^m)T(2^m) и каждое преобразование (2^m) однозначно раскладывается в произведение инвертирующего и перестановочного преобразований =, или, столь же однозначно, - в произведение перестановочного и инвертирующего преобразований =₁₁, где ,₁T(2^m) и ,₁P(2^m).

Доказательство:

1) То, что (2^m)= T(2^m)P(2^m) следует (Курош,50) из перестановочности T(2^m)P(2^m) = P(2^m)T(2^m). Таким образом (2^m) можно представить как произведения ==₁₁, где ,₁T(2^m) и ,₁P(2^m).

2) Если =₁₁=₂₂, то ₁=₂ и ₁=₂. Действительно, из ₁₁=₂₂ следует ₁=₂₂₁^-1 и ₂^-1₁=₂₁^-1, но левая часть этого равенства T(2^m), а правая часть P(2^m) и значит, по теореме 2, ₂^-1₁==₂₁^-1, поэтому ₁=₂ и ₁=₂.

3) Аналогично, если =₁₁=₂₂, то ₁=₂ и ₁=₂. Действительно, из ₁₁=₂₂ следует ₁=₁^-1₂₂и ₁₂^-1=₁^-1₂, но левая часть этого равенства T(2^m), а правая часть P(2^m) и значит, по теореме 2, ₁₂^-1==₁^-1₂, поэтому ₁=₂ и ₁=₂.

Теорема 4.2.3:5: Число логических преобразований порядка 2^m равно произведению числа инвертирующих преобразований порядка 2^m и числа перестановочных преобразований порядка 2^m, то есть 2^m*m!.

Доказательство непосредственно следует из теоремы 4.

Теорема 4.2.3:6: Группа (2^m) имеет систему образующих из трёх преобразований: ₀= (₀), ₁= (₁) и ₀=(1), где

₀=(m-2,m-1,...,3,2,0,1) - транспозиция чисел 0 и 1
₁=(m-2,m-3,...,1,0,m-1) - циклический сдвиг всех элементов

Доказательство:

Поскольку (2^m) можно представить в виде произведения =, где T(2^m) и P(2^m), и поскольку подгруппы T(2^m) и P(2^m) имеют по теоремам 4.2.1:6 и 4.2.2:6 системы образующих, соответственно, {_i}, где iI(m), и {₀,₁}, то эти две системы образующих в совокупности образуют систему {_i,₀,₁} образующих (2^m).

Легко показать, что iI(m) _i=_i0i, где _iP(2^m) и (_i)=(m-1,m-2,...,i+1,0,i-1,...,2,1,i) - транспозиция чисел 0 и i.

Таким образом, (2^m) можно представить в виде произведений ₀, ₁ и _i, где iI(m); далее, раскладываем _i для i>0 в произведение ₀ и перестановочных преобразований; далее каждое перестановочное преобразование раскладываем в произведение ₀, ₁; в результате разложится в произведение трёх преобразований ₀, ₀, ₁. Поэтому система образующих подгруппы (2^m) состоит из трёх преобразований: ₀= (₀), ₁= (₁) и ₀=(1).

4.3. Квадраты.

Определение 4.3:1: Квадратом порядка n назовём матрицу nxn, элементы которой - это все числа из I(n²), то есть каждое целое число от 0 до n²-1 встречается как элемент матрицы и только один раз.

Очевидно, квадрат - это подстановка множества I(n²).

Обозначение 4.3:1: Множество квадратов порядка n обозначим K(n).

Очевидно, K(n)=(n²).

Обозначение 4.3:2: Если kK(n) и i,jI(n), то через k[i,j] обозначим число в i-ой строке и j-ом столбце квадрата k, то есть, учитывая, что k - это подстановка множества I(n²), k[i,j]=(ni+j)k.

4.3.1. Магичность.

Определение 4.3.1:1: Набор n чисел из I(n²) назовём магическим, если сумма этих чисел равна (n²-1)n/2, то есть 1/n от суммы всех чисел из I(n²). Эта сумма (n²-1)n/2 называется магической и обозначается s(n).

Определение 4.3.1:2: Квадрат kK(n) назовём магическим (m-квадратом), если в нём каждая строка, каждый столбец и каждая диагональ - магические, то есть имеют место равенства:

	n-1				n-1
iI(n)		k[i,j]=s(n)		jI(n)		k[i,j]=s(n)
	j=0				i=0
	n-1				n-1
		k[i,i]=s(n)				k[i,n-1-i]=s(n)
	i=0				i=0

Обозначение 4.3.1:1: Множество m-квадратов порядка n обозначим M(n).

4.3.2. Равномерность.

Определение 4.3.2:1: Набор n=2^m чисел x_iI(2^2m), где iI(2^m), назовём равномерным, если в каждом двоичном разряде rI(2m) эти числа имеют поровну "1" и "0", то есть:

	n-1		2m-1
rI(2m)		xi|r =		xi|r = n/2 = 2m-1
	i=0		i=0

Определение 4.3.2:2: Квадрат kK(2^m) назовём равномерным (r-квадратом), если в нём каждая строка, каждый столбец и каждая диагональ равномерные, то есть rI(2m) имеют место равенства:

	2m-1				2m-1
iI(2m)		k[i,j]|r=2m-1		jI(2m)		k[i,j]|r=2m-1
	j=0				i=0
	2m-1				2m-1
		k[i,i]|r=2m-1				k[i,2m-1-i]|r=2m-1
	i=0				i=0

Обозначение 4.3.2:1: Множество r-квадратов порядка 2^m обозначим R(2^m).

4.3.3. Симметричность.

Определение 4.3.3:1: Два числа назовём симметричными порядка n, если их сумма равна n²-1=2s(n)/n.

Теорема 4.3.3:1: Симметричные числа порядка 2^m взаимно-инвертированы, то есть если x+y=(2^m)²-1=2^2m-1, то x=y.

Доказательство очевидно.

Определение 4.3.3:2: Квадрат kK(n) назовём симметричным (c-квадратом), если в его центрально-симметричных клетках находятся симметричные числа порядка n, то есть:

i,jI(n) k[i,j]+ k[n-1-i,n-1-j]=n²-1.

Обозначение 4.3.3:1: Множество c-квадратов порядка n обозначим C(n).

Обозначение 4.3.3:2: Магические равномерные симметричные квадраты будем называть s-квадратами. Множество s-квадратов порядка 2^m обозначим S(2^m)= M(2^m)C(2^m)R(2^m).

4.3.4. Пять типов квадратов 4-го порядка.

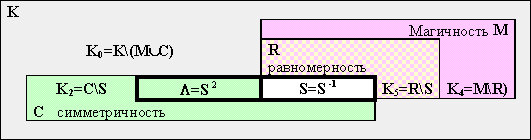
Формально 3 базовых свойства квадрата: магичность, равномерность и симметричность разбивают множество всех квадратов порядка 2^m на 2³=8 подмножеств K_i :

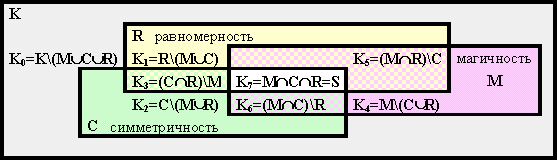
Мы покажем, что при m=2 только 5 из этих множеств непусты: K₀=K\(MCR), K₂=C\(MR), K₄=M\(CR), K₅=(MR)\C, K₇=MCR=S, то есть RM, MCR и S=MCR=MC=CR.

Обозначение 4.3.4:1:

M=M(4)	C=C(4)	R=R(4)	S=S(4)
K=K(4)=(16)=	T=T(16)	P=P(16)	=(16)

Обозначение 4.3.4:2: Шестнадцатиричные цифры будем обозначать так:

Теорема 4.3.4:1: Множество K₀=K\(MCR) непусто, то есть существует числовой квадрат 4-го порядка, не являющийся ни магическим, ни равномерным, ни симметричным.

Теорема 4.3.4:2: Множество K₂=C\(MR) непусто, то есть существует симметричный квадрат 4-го порядка, не являющийся ни магическим, ни равномерным.

Теорема 4.3.4:3: Множество K₄=M\(CR) непусто, то есть существует магический квадрат 4-го порядка, не являющийся ни симметричным, ни равномерным.

Теорема 4.3.4:4: Множество K₅=(MR)\C непусто, то есть существует магический равномерный квадрат 4-го порядка, не являющийся симметричным.

Теорема 4.3.4:5: Множество K₇=MCR=S непусто, то есть существует магический равномерный симметричный квадрат 4-го порядка.

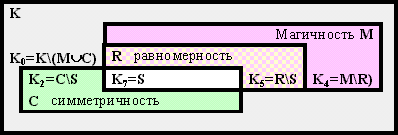
Теорема 4.3.4:6: Равномерный квадрат порядка 2^m является магическим. Как следствие, RM, S=CR. и множества K₁=R\(MC) и K₃=(CR)\M пусты.

Доказательство:

Учитывая разложение числа по степеням двойки (4.1), для ряда (строки, столбца или диагонали) чисел x_i, где iI(2^m), любого квадрата kK(2^m) можно записать:

2m-1

2m-1

2m-1

2m-1

2m-1

2m-1

2m-1

s =

xi

=

2r*(xi|r) =

2r*(xi|r) =

2r

(xi|r)

i=0

i=0

r=0

r=0

i=0

r=0

i=0

		2m-1
Для равномерного квадрата rI(2m)	имеет место равенство	(xi|r)	= 2m-1
		i=0

		2m-1
Поэтому	s =		2r*2m-1 =	(22m -1)*2m-1 = ((22m -1)*2m)/2 = s(2m)
		r=0

Теорема 4.3.4:7: Магический симметричный квадрат 4-го порядка является равномерным, то есть MCR, S=MC и множество K₆=(MC)\R пусто.

Вначале мы докажем три леммы.

Лемма 4.3.4:1: В симметричном магическом квадрате 4-го порядка числа "угловых" подквадратов образуют магический ряд:

k[0,0]		k[0,1]		k[0,2]		k[0,3]		1   1   a,bI(2)        k[2a+i,2b+j] = s(4)     i=0   j=0
	q0				q1
k[1,0]		k[1,1]		k[1,2]		k[1,3]
k[2,0]		k[2,1]		k[2,2]		k[2,3]
	q2				q3
k[3,0]		k[3,1]		k[3,2]		k[3,3]

Доказательство:

При повороте симметричного магического квадрата на 90^o получается, очевидно, тоже симметричный магический квадрат. Поэтому лемму достаточно доказать для подквадрата q₀. С учётом симметричности квадрата k его можно записать в виде (симметричные числа порядка 4 взаимно-инвертированы и их сумма равна F - теорема 4.3.3:1):

k[0,0]	k[0,1]	k[0,2]	k[0,3]
k[1,0]	k[1,1]	k[1,2]	k[1,3]
F- k[1,3]	F- k[1,2]	F- k[1,1]	F- k[1,0]
F- k[0,3]	F- k[0,2]	F- k[0,1]	F- k[0,0]

Запишем условия магичности для строк 0,1 и столбцов 0,1 (для квадрата 4-го порядка s(4)=1E):

k[0,0] + k[0,1] +    k[0,2] +    k[0,3] = 1E
k[1,0] + k[1,1] +    k[1,2] +    k[1,3] = 1E
k[0,0] + k[1,0] + F- k[1,3] + F- k[0,3] = 1E
k[0,1] + k[1,1] + F- k[1,2] + F- k[0,2] = 1E

Складывая эти равенства, получим:

2*( k[0,0] + k[0,1] + k[1,0] + k[1,1]) +4*F = 2*1E

Поэтому k[0,0] + k[0,1] + k[1,0] + k[1,1] = 1E, то есть лемма доказана для подквадрата q₀.

Лемма 4.3.4:2: Диагонали симметричного квадрата 4-го порядка магичны.

Доказательство:

4 клетки диагонали квадрата - это две пары центрально-симметричных клеток. Поэтому на каждой диагонали находятся две пары симметричных чисел 4-го порядка. Сумма чисел каждой пары равна F и поэтому сумма всех четырёх чисел диагонали равна 1E, то есть магической сумме.

Лемма 4.3.4:3: Теорему 7 достаточно доказать для строки 0.

Доказательство:

Учитывая лемму 2, теорему 7 нужно доказывать для строк и столбцов. Доказательство леммы строится на том, что для каждой строки и каждого столбца существует преобразование квадрата, сохраняющее симметричность и магичность квадрата, и такое, что оно переводит эту строку или столбец в строку 0.

Для строки 3, столбцов 0 и 3 такое преобразование - это поворот квадрата на 180^o, 90^o и 270^o по часовой стрелке, соответственно. Для строки 1 это "перекрещивающее" преобразование вида (см. 3.3, преобразование ₁₃):

	k[0,0]k[1,1] k[0,1]k[1,0] k[0,2]k[1,3] k[0,3]k[1,2] k[2,0]k[3,1] k[2,1]k[3,0] k[2,2]k[3,3] k[2,3]k[3,2]	строка 1 строка 0 строка 0 строка 1 строка 3 строка 2 строка 2 строка 3 столбец 1 столбец 0 столбец 0 столбец 1 столбец 3 столбец 2 столбец 2 столбец 3	Диагонали остаются на месте.
			Центрально-симметричные клетки переходят в центрально-симметричные клетки

Для строки 2 и столбцов 1 и 2 такое преобразование - это сочетание "перекрещивающего" преобразования и поворота по часовой стрелке на 180^o, 90^o и 270^o, соответственно.

Доказательство теоремы 7:

Согласно лемме 3 будем доказывать равномерность строки 0.

1) Сначала докажем равномерность строки 0 для двоичного разряда 0, то есть, что в разряде 0 числа строки 0 имеют две "1" и два "0".

Поскольку магическая сумма 4-го порядка чётная (1E), числа любой строки (в том числе и строки 0) должны иметь в 0-м разряде чётное число "1": 0, 2 или 4. Допустим, что в 0-м разряде чисел строки 0 находятся 0 или 4 "1" и постараемся придти к противоречию.

Если в 0-м разряде чисел строки 0 четыре "1", то в строке 3, состоящей из клеток центрально-симметричных клеткам строки 0, числа имеют в 0-м разряде ноль "1" (все четыре "0"). Повернём квадрат на 180^o и будем в новом симметричном магическом квадрате рассматривать строку 0. Итак, можно считать, что в строке 0 числа имеют в 0-м разряде все "0".

Числа строки 1 не могут иметь в 0-м разряде все "0", так как в противном случае мы получаем сумму всех восьми чётных чисел (в строках 0 и 1), равную удвоенной магической сумме 2*1E, а на самом деле она равна 0+2+4+6+8+A+C+E=2*1C.

Точно также числа строки 1 не могут содержать в разряде 0 все "1", так как тогда строка 2 как центрально-симметричная строке 1 состоит из чисел, имеющих в 0-м разряде все "0" и опять сумма всех восьми чётных чисел (в строках 0 и 2) оказывается равной 2*1E, что неверно.

Значит строка 1 содержит 2 чётных и 2 нечётных числа. Поскольку согласно лемме 1 сумма чисел в угловых подквадратах магическая, то есть чётна, очевидно строки 0 и 1 в 0-м разряде выглядят:

0000 или 0000
0011     1100

Из условия симметричности следует, что весь квадрат в 0-м разряде выглядит:

0000 или 0000
0011     1100
1100     0011
1111     1111

В обоих случаях на диагоналях получается нечётное число нечётных чисел, чего быть не может.

Итак, доказано, что числа строки 0 имеют в 0-м разряде две "1" и, соответственно, два "0".

2) При суммировании четырёх чисел строки 0, очевидно, будет перенос "1" в 1-ый разряд и, поскольку, магическая сумма 1E содержит "1" в 1-ом разряде, числа строки 0 должны иметь в 1-ом разряде чётное число "1": 0, 2 или 4.

Рассуждения для разряда 0 теперь полностью повторяются для разряда 1, так как сумма всех восьми чисел, имеющих "0" в 1-ом разряде, равна 0+1+4+5+8+9+C+D=2*1A 2*1E.

3) Рассуждения для разряда 1 повторяются для разряда 2 с учётом того, что сумма всех восьми чисел, имеющих "0" во 2-ом разряде, равна 0+1+2+3+8+9+A+B=2*16 2*1E.

4) Рассуждения для разряда 2 повторяются для разряда 3 с учётом того, что сумма всех восьми чисел, имеющих "0" в 3-ем разряде, равна 0+1+2+3+4+5+6+7=2*10 2*1E.

Итак, теорема 7 доказана.

4.4. Квадраты и преобразования.

4.4.1. Преобразование чисел как преобразование квадратов.

Каждое преобразование чисел (n) естественно расширяется до преобразования квадратов ': K(n)K(n) следующим образом: i,jI(n) k'[i,j]= k[i,j].

Говоря о преобразованиях чисел из (n²) как преобразованиях квадратов, мы будем без специальных оговорок иметь в виду такие расширения.

Теорема 4.4.1:1: Расширение ' есть гомоморфизм группы (n²) преобразований множества I(n²) в группу преобразований множества K(n)=(n²) по операции умножения преобразований: ,(n²) ()'= ''.

Доказательство:

,(n²) i,jI(n) k()'[i,j] = k[i,j]() = (k[i,j]) = (k'[i,j]) = (k')'[i,j] = k('')[i,j].

4.4.2. Квадраты как преобразования. Умножение.

Поскольку квадрат k порядка n - это преобразование (подстановка) множества I(n²), то есть k(n²), то применение к числам квадрата k преобразования (n²) есть, фактически, умножение преобразований k:

i,jI(n) ( k[i,j]) = (по обозначению 4.3:2) = ((ni+j) k) = (ni+j)(k) = (k)[i,j].

4.4.3. Преобразование клеток квадрата.

Преобразование клеток квадрата kK(n) есть, фактически, преобразование множества индексов квадрата, то есть, учитывая, что i,jI(n) [i,j]=(ni+j), множества I(n²). Тем самым (n²).

В результате преобразования число k[i,j] из клетки [i,j] переходит в клетку [i,j], то есть в новом квадрате k' будет k'([i,j])= k[i,j].

k'([i,j]) = k'((ni+j)) = ((ni+j)) k' = (ni+j)(k')
k[i,j] = (ni+j)k

Поэтому (ni+j)(k') = (ni+j)k, то есть k'= k и значит k'=^-1k.

4.4.4. Связь преобразований чисел и клеток квадрата.

Пусть ,(n²), - это преобразование чисел квадрата, - это преобразование клеток квадрата. Эти преобразования дают одинаковый результат для квадрата kK(n)=(n²), если, очевидно, k=^-1k. То есть k=k, или =k^-1-1k, или =k^-1k^-1.

4.4.5. Логические преобразования чисел квадрата.

Теорема 4.4.5:1: Логические преобразования сохраняют равномерность квадрата: kR(2^m) (2^m) kR(2^m).

Доказательство:

Если квадрат порядка 2^m равномерный, то каждая его строка, каждый столбец и каждая диагональ является равномерным набором чисел, то есть:

		2m-1
rI(2m)			xi|r = 2m-1, где iI(2m) и xi22m
		i=0

В силу теоремы 4.2.3:4 достаточно доказать теорему для инвертирующих и перестановочных преобразований.

В результате инвертирующего преобразования (t)T(2^2m) этот набор будет состоять из чисел x_i(t)=x_it и соответствующая поразрядная сумма выглядит так:

		2m-1		2m-1			2m-1,	если t|r=0
rI(2m)			(xit)|r =		(xi|r)(t|r) =					=	2m-1
							2m-2m-1,	если t|r=1
		i=0		i=0

В результате перестановочного преобразования ()P(2^2m) этот набор будет состоять из чисел x_i() и соответствующая поразрядная сумма выглядит так:

		2m-1		2m-1
rI(2m)			(xi())|r =		(xi|r) = 2m-1
		i=0		i=0

Теорема доказана.

Теорема 4.4.5:2: Логические преобразования сохраняют симметричность квадрата: kC(2^m) (2^m) kC(2^m).

Доказательство:

Нужно доказать, что логическое преобразование переводит два симметричных числа порядка 2^m в два симметричных числа того же порядка. В силу теоремы 4.2.3:4 достаточно доказать это для инвертирующих и перестановочных преобразований. Согласно теореме 4.3.3:1 симметричные числа порядка 2^m взаимно-инвертированы, то есть, если x и y симметричны, то x=y.

В результате инвертирующего преобразования (t)T(2^2m), x(t) = xt = (y)t = (по теореме 4.1:1) = (yt) = (y(t)).

В результате перестановочного преобразования ()P(2^2m), rI(2m) (x())|r = (x|r) = (y|r) = (по определению 4.1:2) = (y|r) = (y()).

Теорема доказана.

Теорема 4.4.5:3: Каждый s-квадрат переводится логическим преобразованием в s-квадрат: kS(2^m) (2^m) kS(2^m).

Доказательство непосредственно следует из теоремы 4.3.4:7 и теорем 1,2.

Теорема 4.4.5:4: Если магический квадрат 4-го порядка неравномерный, то существует логическое преобразование, переводящее его в немагический квадрат: kM\R kM.

Доказательство:

Пусть kM\R. Тогда существует ряд (строка, столбец или диагональ) чисел k₀,k₁,k₂,k₃ таких, что:

3		3
ki	= 1E и rI(4) s(k)=	ki|r	2, то есть s(k)=0,1,3,4.
i=0		i=0

Пусть s(k)=0,1. В результате инвертирующего преобразования =(F):

	3
s(k)=	ki|r	=4,3. Для s(k)=0,1,3,4.
	i=0

Пусть s(k)=4. В результате перестановочного преобразования, переводящего разряд r в разряд 3, =(), где

		r,r1,r2,r3		, s(k) =	3
=						ki|3 = 4, то есть iI(4) ki8.
		3,2,1,0
					i=0

Поскольку k_i - это четыре разных числа, то s(k)8+9+A+B=26₁₆>1E.

Пусть теперь s(k)=3. В результате перестановочного преобразования, переводящего разряд r в разряд 0, = (), где

		r,r1,r2,r3		, s(k) =	3
=						ki|0 = 3, то есть s(k) - нечетна и значит не равна 1E.
		0,3,2,1
					i=0

Итак, мы доказали, что преобразование преобразует квадрат k в немагический квадрат.

Теорема 4.4.5:5: R=R, C=C, S=S, MM.

Доказательство:

Поскольку содержит тождественное преобразование, имеем:

RR, CC, SS, MM.
Согласно теоремам 1,2,3,4, RR, CC, SS и M\M.
Поэтому R=R, C=C, S=S, MM.

Теорема 4.4.5:6: Подгруппа логических преобразований разбивает множества R, C, S на непересекающиеся левосторонние смежные классы вида r, c, s, где rR, cC, sS.

Доказательство:

Сначала покажем, что разбивает всё множество квадратов K на непересекающиеся левосторонние смежные классы (это известный факт теории групп).

Если a,bK и ba, то ₀ b=a₀. Тогда ₁,₂ b₁=a(₀₁) и a₂=b(₀^-1₂), то есть b₁a и a₂b. Поэтому два любых левосторонних смежных класса k, где kK, либо совпадают, либо не имеют общих элементов.

Разложение множеств R, C, S на непересекающиеся левосторонние смежные классы по подгруппе следует теперь из теоремы 5.

Теорема 4.4.5:7: Число левосторонних смежных классов множества R равномерных квадратов 4-го порядка по подгруппе логических преобразований равно 11, а множества S симметричных равномерных квадратов 4-го порядка - равно 1:

iI(11) riR i,jI(11) ij riri=, R=		ri   и sS s=S
	i=0

Сначала мы докажем следующее утверждение:

Лемма 4.4.5:1: В любом равномерном квадрате 4-го порядка равномерными являются наборы чисел в подквадратах:

Доказательство:

Пусть rI(4).

a b b a c d d c c d d c a b b a		Рассмотрим картинку, на которой числом x (x=a,b,c,d) помечены клетки квадрата, в которых находят четыре числа x0,x1,x2,x3 такие, что
		3
		xi|r = x
		i=0

Надо доказать, что a=b=c=d=2.
Запишем условия равномерности по разряду r для строк и столбцов квадрата:

Поэтому: 2a = 2d a = d
Условие равномерности по разряду r для диагоналей квадрата: a+d = 2*2 = 4. Поэтому a= d = 2. Следовательно b= 4-a = 2, c = 4-a = 2.

Доказательство теоремы 7:

1) Для любого квадрата kR можно найти инвертирующее преобразование T такое, что k[1,1]=F. Действительно, для t() = k[1,1], k[1,1] = k[1,1]k[1,1] = ( k[1,1]k[1,1])= 0 = F. Поэтому далее будем рассматривать квадрат k₁=k, в котором k₁[1,1]=F.

2) Существует перестановочное преобразование ₁P такое, что k₁₁[2,2] = 0,8,C,E. (₁) в зависимости от k₁[2,2] определяется так:

(3210): 00		(3210): 8 8		(3210): C C		(3210): E E
		(2310): 4 8		(3120): A C		(3201): D E
		(1230): 2 8		(3012): 9 C		(3012): B E
		(0213): 1 8		(1230): 6 C		(0213): 7 E
				(0213): 5 C
				(1032): 3 C

Поэтому далее будем рассматривать квадрат k₂ = k₁₁, в котором k₂[2,2] = 0,8,C,E.

1		2			3			4
F         0		F         8	на главной диагонали две "1" в разряде 3		F         C	на главной диагонали две "1" в разрядах 3,2		F         E	на главной диагонали две "1" в разрядах 3,2,1

3) Существует перестановочное преобразование ₂P такое, что центральный подквадрат в квадрате k₃ = k₂₂, с учётом его равномерности, имеет один из 12 типов. Квадрат k₃ имеет вид:

1.1	1.2	1.3
F E     1 0	F C     3 0	F 1     E 0		(2) - перестановка разрядов 3,2,1,0, не изменяющая числа F,0 и переводящая число k2[1,2] в нужное; число k2[2,1] вычисляется из условия равномерности подквадрата
2.1	2.2	2.3	2.4
F 7     0 8	F 6     1 8	F 1     6 8	F 0     7 8	(2) - перестановка разрядов 2,1,0, не изменяющая числа F,8 и переводящая число k2[1,2] в нужное; число k2[2,1] вычисляется из условия равномерности подквадрата
3.1	3.2	3.3
F 3     0 C	F 2     1 C	F 0     3 C		(2) - перестановка разрядов 1,0, не изменяющая числа F,C и переводящая число k2[1,2] в нужное; число k2[2,1] вычисляется из условия равномерности подквадрата
4.1	4.2
F 1     0 E	F 0     1 E			2=; числа k2[1,2] и k2[2,1] вычисляются из условия равномерности подквадрата

Рассмотрим все эти случае по порядку.

4) Квадрат k₃ имеет вид:

5) Квадрат k₃ имеет вид:

6) Квадрат k₃ имеет вид:

Перестановкой ₃ разрядов 1,0, не изменяющей уже имеющиеся в квадрате числа F,C,3,0, можно добиться , чтобы в квадрате k₃=k₂(₃) было x=2, y=1.

Перестановкой ₄ разрядов 3,2, не изменяющей уже имеющиеся в квадрате числа F,C,3,2,1,0, можно добиться , чтобы в квадрате k₄=k₃(₄) было x=8, y=4.

Для вариантов 3.1, 3.3 число "y" стоит в ряду, где уже есть два чётных числа 2,8. Поэтому y - нечётно, то есть x=E, y=D.

Для варианта 1.2 рассмотрим квадрат k|0 ( i,jI(4) (k|0)[i,j]=k[i,j]|0 ). v= k[0,0]|0, w=v, t=y|0.

1.2|0 (0-й разряд квадрата 1.2)
v 0      0 1 0 1   3 0 t   4	равномерность столбца 2	v 0 1    0 1 0 1   3 0 t   4 1	равномерность столбца 0 и главной диагонали	v 0 1 w 0 1 0 1   3 0 t   4 1 w	равномерность столбца 3	v 0 1 w 0 1 0 1   3 0 1   4 1 w

Таким образом y|0=t=1, то есть в варианте 1.2 тоже y - нечётно, и x=E, y=D.

Число x стоит в ряду, в котором уже есть два чётных числа 2,E. Поэтому x - нечётно, то есть x=5, y=A или x=9, y=6.

1.2.1	1.2.2	3.1.1	3.1.2	3.3.1	3.3.2
5 8      2 F C 1 E 3 0 D   4   y	9 8      2 F C 1 E 3 0 D   4   6	2 5   E 8 F 3 4   0 C   D A   1	2 9   E 8 F 3 4   0 C   D 6   1	2 8   D 5 F 0 A   3 C   E 4   1	2 8   D 9 F 0 6   3 C   E 4   1	Достроим эти квадраты с помощью условий равномерности (или магичности).

Таким образом, первые 5 квадратов m₀, m₁, m₂, m₃, m₄.

7) Квадрат k₃ имеет вид:

Условие равномерности ряда u, 1, 8, z: u+z=F+6=E+7. Числа F, 6 уже есть в квадрате. Таким образом u=E, z=7 или u=7, z=E.

Рассмотрим для обоих вариантов 2.2, 2.3 квадраты k|0 ( i,jI(4) (k|0)[i,j]= k[i,j]|0). v=k[0,0]|0, w=v, t=y|0, s=z|0.

2.2|0=2.3|0 (0-й разряд квадратов 2.2, 2.3)
v          1 0 t   1 0 s	равномерность столбцов 1, 2	v 0 1      1 0 t   1 0 s   0 1	равномерность строки 0 и главной диагонали	v 0 1 w   1 0 t   1 0 s       w	равномерность столбца 3	v 0 1 w   1 0 v   1 0 v       w

Таким образом, y|0=t=v=s=z|0, то есть y и z одинаковой чётности. Поэтому x=0, y=9, u=E, z=7 или x=9, y=0, u=7, z=E.

Число x стоит в ряду, в котором уже есть два чётных числа 0,E. Поэтому x - нечётно, то есть x=5, y=2 или x=3, y=4.

Перестановкой ₃ разрядов 2,1, не изменяющей уже имеющиеся в квадрате числа F,E,9,8,7,6,1,0 можно добиться , чтобы в квадрате k₃=k₂(₃) было x=5, y=2.

Число x стоит в ряду, в котором уже есть два числа, имеющие "1" в разряде 2: 5|2=C|2=1. Поэтому x|2=0, то есть x=A, y=4.

8) Квадрат k₃ имеет вид:

Рассмотрим квадрат k|0 ( i,jI(4) ( k|0)[i,j]= k[i,j]|0). v=x|0, w= v, s=u|0.

Таким образом, x|0=v, u|0=s=w=v, то есть x и u разной чётности. Поэтому x=0, y=3, u=D, z=E или x=3, y=0, u=E, z=D.

Число x стоит в ряду, в котором уже есть два нечётных числа F,1. Поэтому x - чётно, то есть x=4, y=9 или x=8, y=5.

Перестановкой ₃ разрядов 3,2, не изменяющей уже имеющиеся в квадрате числа F,E,D,C,3,2,1, можно добиться , чтобы в квадрате k₃=k₂(₃) было x=4, y=9.

Число x стоит в ряду, в котором уже есть два нечётных числа 3,D. Поэтому x - чётно, то есть x=8, y=5.

9) Итак, мы получили 11 квадратов

Сам способ их построения гарантирует, что они относятся к разным левосторонним смежным классам множества R равномерных квадратов 4-го порядка по подгруппе логических преобразований. Можно преобразовать их к виду, когда число 0 находится в клетке [0,0], а числа 1,2,4,8 встречаются именно в таком порядке при считывании чисел квадрата по строкам сверху вниз (в порядке возрастания [i,j]=4i+j). Очевидно, что никакими логическими преобразованиями такие квадраты друг в друга перейти не могут.

r_i = m_i(t_i)(_i)

ti =	5	2	2	2	2	5	2	5	2	3	0
i =	(1032)	(2310)	(3210)	(2031)	(3021)	(3012)	(0312)	(1302)	(1023)	(2310)	(2031)
	0 7 B C D A 6 1 E 9 5 2 3 4 8 F	0 B 7 C 6 D 1 A 9 2 E 5 F 4 8 3	0 B 7 C A D 1 6 5 2 E 9 F 4 8 3	0 3 C F D E 1 2 7 4 B 8 A 9 6 5	0 9 6 F D E 1 2 7 4 B 8 A 3 C 5	0 F 3 C 5 A 6 9 E 1 D 2 B 4 8 7	0 3 F C E D 1 2 D A 6 5 7 4 8 B	0 3 E D F C 1 2 9 A 7 4 6 5 8 B	0 D 6 B A 7 1 C F 2 9 4 5 8 3 E	0 B 6 D 7 C 1 A 9 2 F 4 E 5 8 3	0 3 D E C F 1 2 7 4 A 9 B 8 6 5
	r0	r1	r2	r3	r4	r5	r6	r7	r8	r9	r10

10) Только один из этих одиннадцати квадратов является симметричным - квадрат r₀. Поэтому существует только один левосторонний смежный класс множества S по подгруппе : sS s=S.

4.4.6. Логические преобразования клеток квадрата.

Теорема 4.4.6:1: Логическое преобразование клеток равномерного симметричного квадрата 4-го порядка переводит его также в равномерный симметричный квадрат, то есть (согласно 4.4.3): sS ^-1sS.

Доказательство:

1) Теорему достаточно доказать для одного (любого) s₀S. Действительно, в силу теоремы 4.4.5:7 sS ₀ s=s₀₀. Поэтому, если s₁=^-1s₀S, то ^-1s = ^-1(s₀₀) = (^-1s₀)₀ = s₁₀ S.

2) Поскольку имеет, согласно теореме 4.2.3:6, систему образующих { ₀, ₁, ₀}, где (₀)=₀=(3201), (₁)=₁=(2103), t(₀)=1, то теорему достаточно доказать для ₀s₀, ₁s₀, ₀s₀.

Соответствующие им преобразования клеток, согласно 4.4.3, ₀^-1, ₁^-1, ₀^-1:

(₀^-1) = ₀^-1 = ₀ = (3201)
(₁^-1) = ₁^-1 = (0321)
t(₀^-1) = t(₀) = 1

0-1

1-1

0-1

3) Для квадрата r₀ из теоремы 4.4.5:7 имеем:

r0 =

0 7 B C D A 6 1 E 9 5 2 3 4 8 F

0r0 =

0 B 7 C D 6 A 1 E 5 9 2 3 8 4 F

1r0 =

0 7 D A E 9 3 4 B C 6 1 5 2 8 F

0r0 =

7 0 C B A D 1 6 9 E 2 5 4 3 F 8

Симметричность и равномерность (или магичность) этих квадратов проверяется непосредственно.

Теорема 4.4.6:2: Существует логическое преобразование клеток квадрата, которое каждый несимметричный квадрат r_i из теоремы 4.4.5:7 переводит в немагический квадрат, то есть (согласно 4.4.3) ^-1r_iM.

Доказательство:

Рассмотрим преобразование ₀, ₀(₀)=₀=(3201). Соответствующее ему преобразование клеток ₀^-1=₀ переставляет местами столбцы 1 и 2. Для квадратов r₁r₁₀ из теоремы 4.4.5:7 главная диагональ квадратов ₀r₁₀r₁₀ не является магической:

0r1 : 0123		0r3 : 0145		0r5 : 0617		0r7 : 01AB		0r9 : 0123
0r2 : 0123		0r4 : 0145		0r6 : 01AB		0r8 : 012E		0r10 : 0145

Теорема 4.4.6:3: Если равномерный квадрат 4-го порядка не является симметричным, то существует логическое преобразование клеток, переводящее его в неравномерный квадрат, то есть (согласно 4.4.3) rR\S ^-1rR.

Доказательство:

1) В силу теоремы 4.4.5:7 теорему достаточно доказать для любых представителей r_i левосторонних смежных классов R\ S по подгруппе .

Действительно, rR iI(11) ₀ r=r_i0.
Поэтому, если k=r_iR, то r=(r_i0)=(r_i)₀=k₀.
Очевидно, что k₀R, так как иначе, если k₀R, то (k₀)₀^-1R и значит kR, что неверно.

2) В силу теоремы 2 теорема 3 доказана.

Теорема 4.4.6:4: Логическое преобразование клеток симметричного квадрата 4-го порядка переводит его также в симметричный квадрат, то есть (согласно 4.4.3) cC ^-1cC.

Доказательство:

Достаточно проверить, что 3 преобразования клеток, соответствующие образующим преобразованиям ₀, ₁, ₀, переводят центрально-симметричные клетки квадрата в центрально-симметричные клетки. Это непосредственно видно по их схемам (доказательство теоремы 1).

Теорема 4.4.6:5: S=S, C=C, R=R, MM.

Доказательство:

Поскольку содержит тождественное преобразование, имеем: SS, CC, RR, MM.
Согласно теоремам 14 SS, CC, RR, M\M.
Поэтому S=S, C=C, R=R, MM.

4.4.7. Симметричные магические квадраты.

Теорема 4.4.7:1: sS s=s=S=S=S=S=S.

Доказательство:

1) По теореме 4.4.5:7 sS s=S. Поскольку и S конечные множества, то число логических преобразований равно числу s-квадратов.

2) По теореме 4.4.5:5 S= S. По теореме 4.4.6:5 S=S.

3) Из 2) вытекает sS sS=S, SS=S, SS=S. В силу равномощности конечных множеств и S имеем s=S=S=S.

Теорема 4.4.7:2: S^-1=S.

Доказательство:

1) Для квадрата Дюрера имеем

sd = sd-1 =

F 2 1 C 4 9 A 7 8 5 6 B 3 E D 0

2) Согласно теореме 4.4.5:7 sS s=s_d. Поэтому s^-1 = (s_d)^-1 = ^-1s_d^-1 = ^-1s_d. Согласно теореме 1, поскольку ^-1, ^-1s_dS, то есть s^-1S.

3) Итак, S^-1S. В силу конечности S имеем S^-1=S

Теорема 4.4.7:3: sS 7е sS=Ss=S²=.

Доказательство:

1) s,s₁S s^-1s₁.
Действительно, s,s₁S ss₁=s. Поэтому s^-1s₁=, то есть s^-1s₁.

2) s,s₁S ss₁.
Действительно, s,s₁S ss₁=(s^-1)^-1s₁. Согласно теореме 2 s^-1S. По 1) (s^-1)^-1s₁, то есть ss₁.

3) Из 2) следует, что sS sS, Ssи S²=SS. В группе всех преобразований K, как во всякой группе, s,s₁,s₂SK s₁s₂ ss₁ss₂ . Следовательно, поскольку множества sS, Ss и S конечные, они имеют одинаковое число элементов. Поскольку, в свою очередь, число логических преобразований равно числу s-квадратов, получаем, что sS=, Ss= и S²=SS=.