|
|
разряды
|
обозначение
|
название
|
выражение через
|
выражение через
|
|
|
3210
|
||||||
|
код
функции |
x =
|
0011
|
& и
|
|
||
|
y =
|
0101
|
|
|
|||
|
0
|
KA |
0000
|
0
|
ложь
|
0
|
0
0 |
|
1
|
KA |
0001
|
x&y
|
конъюнкция
|
x&y
|
(x
(x |
|
2
|
0010
|
x\y
|
разность
|
x&
|
(x
(x |
|
|
3
|
A |
0011
|
x
|
x
|
x
|
x
x |
|
4
|
0100
|
y\x
|
разность
|
|
x
((x |
|
|
5
|
A |
0101
|
y
|
y
|
y
|
y
y |
|
6
|
KA |
0110
|
x
|
исключающая
дизъюнкция |
(x&
(x |
(x
(x |
|
7
|
KA |
0111
|
x
|
дизъюнкция
|
x
|
(x
(x |
|
8
|
K |
1000
|
x
|
стрелка Пирса
|
|
x
((x |
|
9
|
KA |
1001
|
x
|
эквивалентность
|
(x&y)
( |
(x
(x |
|
A
|
1010
|
|
отрицание
|
|
y
y |
|
|
B
|
1011
|
y
|
импликация
|
x
|
((x
(x |
|
|
C
|
1100
|
|
отрицание
|
|
x
x |
|
|
D
|
1101
|
x
|
импликация
|
|
(x
x |
|
|
E
|
K |
1110
|
x
|
штрих Шеффера
|
|
((x
x |
|
F
|
KA |
1111
|
1
|
истина
|
1
|
1
|
K - коммутативные операции, A - ассоциативные операции
Возьмём магический квадрат 4x4, изображённый на знаменитой картине Дюрера:
16 3 2 13 Вычитаем "1" из каждого числа и преобразуем десятичные числа в шестнадцатиричные
F 2 1 C 5 10 11 8 4 9 A 7 9 6 7 12 8 5 6 B 4 15 14 1 3 E D 0
Подставив вместо чисел обозначения соответствующих логических операций, получаем:
x
y
y
y
y
y
x
y
y
Используя выражения логических операций через &, ![]() ,
,
![]() , можно записать:
, можно записать:
y
x
x&y
(
x&
y)
y
y
x&
y
y)
(
x&y)
y
x
y
x
y
Ниже, если не оговорено особо, под квадратом d будетпониматься
квадрат, составленный из шестнадцатиричных чисел 0![]() F,
или квадрат логических функций. Магическая сумма такого квадрата равна 1E16.
F,
или квадрат логических функций. Магическая сумма такого квадрата равна 1E16.
Квадрат d обладает глубокой симметрией, исследованию которой посвящены подпункты п.2.3.
Желтым цветом выделены все коммутативные операции. Коммутативные и некоммутативные операции заполняют квадрат в шахматном порядке. Главная диагональ - коммутативные операции, вторая диагональ - некоммутативные операции.
|
d1=d |
|
d2=d |
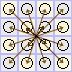 |
|
d3=d |
 |
|
d4=d |
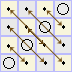 |
|
d5=d |
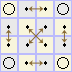 |
|
d6=d |
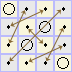 |
|
d7=d |
квадрат d7 =
|
|
| В квадрате d7 можно выделить 4 подквадрата 2x2 по схеме: |
Эти подквадраты r7i квадрата d7 выглядят так: | ||||||||||||
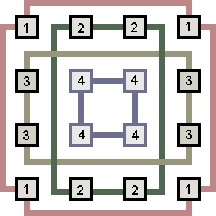 |
r71
|
|
|
r72
|
r71 = r74 r72 = r73 r71 = |
||||||||
|
r73
|
|
|
r74
|
||||||||||
| r71 и r72 получаются друг из друга с помощью центрально-симметричного преобразования - операцией отрицания. | |||||||||||||
| В квадрате d7 можно выделить 4 подквадрата 2x2 по схеме: |
Эти подквадраты q7i квадрата d7 выглядят так: | ||||||||||||||||||||||||||||||||
|
q71
|
|
|
q72
|
q71 = q72 = q71 = q72(1) = q73(0) q74 = q72(0) = q73(1) |
||||||||||||||||||||||||||||
|
q73
|
|
|
q74
|
||||||||||||||||||||||||||||||
Подквадраты ri квадрата d, соответствующие подквадратам r7i квадрата d7. Каждый из этих квадратов имеет структуру вида:
|
Более детально:
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Преобразование ![]() 3
: d3(x,y)=d(
3
: d3(x,y)=d(![]() x,
x,![]() y)
преобразует r2 в r3`, отличающийся от r3
симметрией относительно главной диагонали подквадрата r3 (и
наоборот):
y)
преобразует r2 в r3`, отличающийся от r3
симметрией относительно главной диагонали подквадрата r3 (и
наоборот):
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Преобразование ![]() 4
: d4(x,y)=
4
: d4(x,y)=![]() d(
d(![]() x,
x,![]() y)
преобразует r2 в r3``, отличающийся от r3
симметрией относительно второй диагонали подквадрата r3 (и
наоборот):
y)
преобразует r2 в r3``, отличающийся от r3
симметрией относительно второй диагонали подквадрата r3 (и
наоборот):
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Преобразование ![]() 6
: d6(x,y)=d(
6
: d6(x,y)=d(![]() x,y)
преобразует r2 в r3```, отличающийся от
r3 поворотом на 90o:
x,y)
преобразует r2 в r3```, отличающийся от
r3 поворотом на 90o:
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Преобразование ![]() 7
: d7(x,y)=d(x,x) преобразует r4 в
r1.
7
: d7(x,y)=d(x,x) преобразует r4 в
r1.
Можно применить штрих Шеффера по схеме:
|
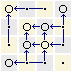 |
r11 = |
r41 = r3x r4x = r31 |
Можно применить стрелку Пирса по симметричной схеме:
|
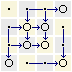 |
|
r4x = |
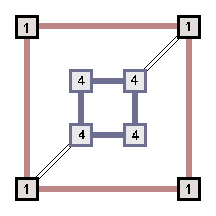
Преобразование ![]() 1
: d1(x,y)=d(y,x) объединяет квадраты r2
и r3 в конструкцию слева и квадраты r1 и r4
в конструкцию справа:
1
: d1(x,y)=d(y,x) объединяет квадраты r2
и r3 в конструкцию слева и квадраты r1 и r4
в конструкцию справа:
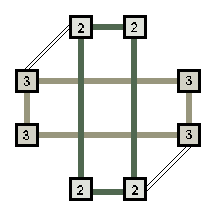 |
 |
В применении к строкам, столбцам и диагоналям квадрата d эти операции дают:
| & конъюнкция | - 0 |
| - 1 | |
| - 1 | |
| - 0 |
Если из исходного квадрата d, составленного из шестнадцатиричных цифр, построить 4 поразрядных квадрата, то получится, что в каждом из этих квадратов в каждой строке, каждом столбце и на каждой диагонали ровно два "0" и две "1":
| квадрат d | разряд 3 | разряд 2 | разряд 1 | разряд 0 |
| F21C 49A7 856B 3ED0 |
1010 0101 0101 1010 |
1100 0011 0011 1100 |
1001 1001 0110 0110 |
1001 0110 1001 0110 |
К исходному квадрату d, составленному из шестнадцатиричных чисел, можно
поразрядно применить операцию ![]() a.
Для a=6,B,D имеем:
a.
Для a=6,B,D имеем:
| a=6 | r1 r4 r4 |
r2 r3 r3 |
|
|||||||||||||||||||||||||
| a=B | r1 r3 r3 |
r2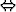 r4 r4 |
||||||||||||||||||||||||||
| a=D | r1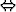 r2 r2 |
r3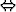 r4 r4 |
Подквадраты qi квадрата d, соответствующие подквадратам q7i квадрата d7. Каждый из этих подквадратов имеет структуру вида:
|
или
|
|
причем b(x,y)=a(y,x)
|
Более детально:
| q1b | q2a | ||
| q1a | q2b | ||
| q3a | q4b | ||
| q3b | q4a |
Квадраты qi переходят друг в друга в результате применения
к квадрату d как квадрату шестнадцатиричных чисел поразрядной операции
![]() a, где a=7,9,E:
a, где a=7,9,E:
| a=9 | q1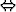 q4 q4 |
q2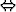 q3 q3 |
|
|||||||||||||||||||||||||
| a=7 | q1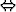 q3 q3 |
q2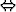 q4 q4 |
||||||||||||||||||||||||||
| a=E | q1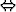 q2 q2 |
q3 q4 q4 |
Эти преобразования переводят магический квадрат Дюрера d тоже в магический
квадрат (естественно, с той же магической суммой 1E16 - для квадрата
шестнадцатиричных чисел 7![]() F).
F).
Это преобразование конструирует из магического квадрата d обобщённый магический квадрат с той же магической суммой, составленный из 4-х чисел 0,3,C,F, каждое из которых встречается ровно 4 раза и при этом один раз в каждой строке и каждом столбце. Диагонали составлены каждая из двух чисел (0,F) и (3,C), встречающихся на диагонали 2 раза.
|
квадрат d
|
схемы расположения чисел:
|
|||||||||||||||||||
| F | 0 | C | 3 | |||||||||||||||||
|
 |
 |
 |
 |
||||||||||||||||
Каждый из этих подквадратов состоит из 4-х чисел, сумма которых равна магической сумме 1E.
Центрально-симметричные клетки квадрата d и подквадратов r1![]() r4
и q1
r4
и q1![]() q4.
Сумма каждых двух центрально-симметричных чисел магического квадрата d
(расположенных в центрально-симметричных клетках квадрата) равна половине магической
суммы 1E/2=F. Соответственно, это относится к сумме центрально-симметричных
чисел каждого подквадрата r1
q4.
Сумма каждых двух центрально-симметричных чисел магического квадрата d
(расположенных в центрально-симметричных клетках квадрата) равна половине магической
суммы 1E/2=F. Соответственно, это относится к сумме центрально-симметричных
чисел каждого подквадрата r1![]() r4.
Суммы центрально-симметричных чисел подквадратов q1
r4.
Суммы центрально-симметричных чисел подквадратов q1![]() q4
равны 6-18 и 8-16 и располагаются по схеме:
q4
равны 6-18 и 8-16 и располагаются по схеме:
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||